Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sohrabi, S.
and
Ranjbar, H.
2019.
On Sinc discretization for systems of Volterra integral-algebraic equations.
Applied Mathematics and Computation,
Vol. 346,
Issue. ,
p.
193.
Gao, Hecong
and
Liang, Hui
2022.
Discontinuous piecewise polynomial collocation methods for integral-algebraic equations of Hessenberg type.
Computational and Applied Mathematics,
Vol. 41,
Issue. 6,
Sajjadi, Sayed Arsalan
Najafi, Hashem Saberi
and
Aminikhah, Hossein
2023.
A numerical algorithm for solving index-1 weakly singular integral-algebraic equations with non-smooth solutions.
Applicable Analysis,
Vol. 102,
Issue. 13,
p.
3733.
Bagomghaleh, Shadi Malek
Pishbin, Saeed
and
Gholami, Gholamhossein
2024.
Numerical and analytical findings on the Volterra integral-algebraic index-1 system with vanishing delays.
Applied Mathematics and Computation,
Vol. 466,
Issue. ,
p.
128449.


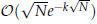 . Moreover, Sinc method is applied to several examples to illustrate the accuracy and implementation of the method.
. Moreover, Sinc method is applied to several examples to illustrate the accuracy and implementation of the method.