Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T08:21:22.023Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Two-Grid Method for Expanded Mixed Finite Element Solution of Nonlinear Reaction Diffusion Equations

Part of: Partial differential equations, initial value and time-dependent initial-boundary value problems Partial differential equations, boundary value problems

Published online by Cambridge University Press:  17 January 2017

Shang Liu  and
Yanping Chen
Shang Liu*
Affiliation:
School of Mathematics and Computational Science, Xiangtan University, Xiangtan 411105, Hunan, China School of Mathematics and Computational Science, Changsha University of Science and Technology, Changsha 410114, Hunan, China
Yanping Chen*
Affiliation:
School of Mathematical Science, South China Normal University, Guangzhou 520631, Guangdong, China
*
*Corresponding author. Email:[email protected] (S. Liu), [email protected] (Y. P. Chen)
*Corresponding author. Email:[email protected] (S. Liu), [email protected] (Y. P. Chen)
Get access

Abstract

In the paper, we present an efficient two-grid method for the approximation of two-dimensional nonlinear reaction-diffusion equations using a expanded mixed finite-element method. We transfer the nonlinear reaction diffusion equation into first order nonlinear equations. The solution of the nonlinear system on the fine space is reduced to the solutions of two small (one linear and one non-linear) systems on the coarse space and a linear system on the fine space. Moreover, we obtain the error estimation for the two-grid algorithm. It is showed that coarse space can be extremely coarse and achieve asymptotically optimal approximation as long as the mesh sizes satisfy 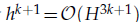. An numerical example is also given to illustrate the effectiveness of the algorithm.

Keywords

Error estimationmixed finite elementsreaction-diffusion equationstwo-grid methods

MSC classification

Secondary: 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods 65N15: Error bounds 65M12: Stability and convergence of numerical methods
Type
Research Article
Information
Advances in Applied Mathematics and Mechanics , Volume 9 , Issue 3 , June 2017 , pp. 757 - 774
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Brezzi, F. Jr. Douglas, J. and Marini, L. D., Two families of mixed finite element for second order elliptic problems, Numerische Mathematic, 47 (1985), pp. 217–235.Google Scholar
[2] Brezzi, F. and Fortin, M., Mixed and Hybrid Finite Element Methods, Springer-Verlag, 1991.CrossRefGoogle Scholar
[3] Ewing, R. E., Lazarov, R. D. and Wang, J., Superconvergence of the velocity along the Gauss lines in mixed finite element methods, SIAM J. Numer. Anal., 28 (1991), pp. 1015–1029.CrossRefGoogle Scholar
[4] He, Y. and Li, J., Convergence of three iterative methods based on the finite element discretization for the stationary Navier-Stokes equations, Comput. Methods Appl. Mech. Eng., 15 (2009), pp. 1351–1359.Google Scholar
[5] Liu, Qingfang and Hou, Yanren, A two-level finite element method for the Navier-Stokes equations based on a new projection, Appl. Math. Model., 34(2) (2010), pp. 383–399.CrossRefGoogle Scholar
[6] Hou, Yanren and Li, Kaitai, Postprocessing fourier Galerkin method for the Navier-Stokes equations, SIAM J. Numer. Anal., 47(3) (2009), pp. 1909–1922.Google Scholar
[7] Chen, Y. and Huang, Y., A multilevel iterate correction method for solving nonlinear singular problems, Natural Science Jounal of Xiangtan Univ., 16 (1994), pp. 23–26 (in Chinese).Google Scholar
[8] Chen, Y., Huang, Y. and Yu, D., A two-grid method for expanded mixed finite-element solution of semilinear reaction-diffusion equations, Int. J. Numer. Meth. Eng., 57 (2003), pp. 193–209.Google Scholar
[9] Chen, Y., Liu, H. and Liu, S., Analysis of two-grid methods for reaction-diffusion equations by expanded mixed finite element methods, Int. J. Numer. Meth. Eng., 69 (2007), pp. 408–422.Google Scholar
[10] Chen, Y., Luan, P. and Lu, Z., Analysis of two-grid methods for nonlinear parabolic equations by expanded mixed finite element methods, Adv. Appl. Math. Mech., 1 (2009), pp. 1–15.CrossRefGoogle Scholar
[11] Chen, L. P. and Chen, Y., Two-grid method for nonlinear reaction-diffusion equations by mixed finite element methods, J. Sci. Comput., 47 (2011), pp. 383–401.CrossRefGoogle Scholar
[12] Dawson, C. N. and Wheeler, M. F., Two-grid methods for mixed finite element approximations of non-linear parabolic equations, Contemporary Mathematics, 180 (1994), pp. 191–203.Google Scholar
[13] Dawson, C. N., Wheeler, M. F. and Woodward, C. S., A two-grid finite difference scheme for non-linear parabolic equations, SIAM J. Numer. Anal., 35 (1998), pp. 435–452.Google Scholar
[14] Douglas, J. Jr., Ewing, R. E. and Wheeler, M. F., The approximation of the pressure by a mixed method in the simulation of miscible displacement, RAIRO, Analyse Numérique, 17 (1983), pp. 17–33.Google Scholar
[15] Huyakorn, P. S. and Pinder, G. F., Computational Methods in Subsurface Flow, Academic Press, New York, 1983.Google Scholar
[16] Huang, Y., Shi, ZH., Tang, T. and Xue, W., A multilevel successive iteration method for non-linear elliptic problems, Math. Comput., 73(246) (2004), pp. 525–539.CrossRefGoogle Scholar
[17] Huang, Y. and Xue, W., Convergence of finite element approximations and multilevel linearization for Ginzburg-Landau model of D-wave superconductors, Adv. Comput. Math., 17 (2002), pp. 309–330.CrossRefGoogle Scholar
[18] Milner, F., Mixed finite element methods for quasilinar second-order elliptic problems, Math. Comput., 44 (1985), pp. 302–320.Google Scholar
[19] Murray, J., Mathamatical Biology, 2nd edn, Springer, New York, 1993.CrossRefGoogle Scholar
[20] Raviart, P. A. and Thomas, J. M., A mixed finite element method for 2nd order elliptic problems, Math. Aspects of the Finite Element Method, Lecture Notes in Math., 606 (Springer, Berlin, 1977), pp. 292–315.Google Scholar
[21] Wu, L. and Allen, M. B., A two-grid method for mixed finite-element solution of reaction-diffusion equations, Numerical Methods for Partial Differntial Equations, 15 (1999), pp. 317–332.Google Scholar
[22] Xu, J., A novel two-grid method for semilinear equations, SIAM J. Sci. Comput., 15 (1994), pp. 231–237.Google Scholar
[23] Xu, J., Two-grid discretization techniques for linear and non-linear PDEs, SIAM J. Numer. Anal., 33 (1996), pp. 1759–1777.Google Scholar