Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T19:02:35.287Z Has data issue: false hasContentIssue false
  • English
  • Français

A High-Efficient Algorithm for Parabolic Problems with Time-Dependent Coefficients

Part of: Partial differential equations, initial value and time-dependent initial-boundary value problems Acceleration of convergence Partial differential equations, boundary value problems

Published online by Cambridge University Press:  09 January 2017

Chuanmiao Chen ,
Xiangqi Wang  and
Hongling Hu
Chuanmiao Chen*
Affiliation:
College of Mathematics and Computer Science, Key Laboratory of High Performance Computing and Stochastic Information Processing, Hunan Normal University, Changsha, Hunan 410081, China
Xiangqi Wang*
Affiliation:
College of Mathematics and Computer Science, Key Laboratory of High Performance Computing and Stochastic Information Processing, Hunan Normal University, Changsha, Hunan 410081, China
Hongling Hu
Affiliation:
College of Mathematics and Computer Science, Key Laboratory of High Performance Computing and Stochastic Information Processing, Hunan Normal University, Changsha, Hunan 410081, China
*
*Corresponding author. Email:[email protected] (C. M. Chen), [email protected] (X. Q. Wang)
*Corresponding author. Email:[email protected] (C. M. Chen), [email protected] (X. Q. Wang)
Get access

Abstract

A high-efficient algorithm to solve Crank-Nicolson scheme for variable coefficient parabolic problems is studied in this paper, which consists of the Function Time-Extrapolation Algorithm (FTEA) and Matrix Time-Extrapolation Algorithm (MTEA). First, FTEA takes a linear combination of previous l level solutions 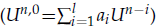as good initial value of Un(see Time-extrapolation algorithm (TEA) for linear parabolic problems, J. Comput. Math., 32(2) (2014), pp. 183–194), so that Conjugate Gradient (CG)-iteration counts decrease to 1/3~1/4 of direct CG. Second, MTEA uses a linear combination of exact matrix values in level L, L+s, L+2s to predict matrix values in the following s–1 levels, and the coefficients of the linear combination is deduced by the quadric interpolation formula, then fully recalculate the matrix values at time level L+3s, and continue like this iteratively. Therefore, the number of computing the full matrix decreases by a factor 1/s. Last, the MTEA is analyzed in detail and the effectiveness of new method is verified by numerical experiments.

Keywords

Crank-Nicolson schemeTime-ExtrapolationCG-iterationvariable coefficient parabolic

MSC classification

Secondary: 65M06: Finite difference methods 65M12: Stability and convergence of numerical methods 65B05: Extrapolation to the limit, deferred corrections 65N22: Solution of discretized equations
Type
Research Article
Information
Advances in Applied Mathematics and Mechanics , Volume 9 , Issue 2 , April 2017 , pp. 501 - 514
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Brandt, A., Multi-level adaptive solutions to boundary value problems, Math. Comput., 31 (1977), pp. 333–390.CrossRefGoogle Scholar
[2] Bornemann, F. and Deuflhard, P., The cascadic multigrid method for elliptic problems, Numer. Math., 75(2) (1996), pp. 135–152.CrossRefGoogle Scholar
[3] Chen, C. M. and Huang, Y. Q., High Accuracy Theorey of Finite Elements, Changsha: Hunan Science and Technique Press, 1995.Google Scholar
[4] Chen, C. M., Hu, H. L., Xie, Z. Q. and Li, C. L., Analysis of extrapolation cascadic multigrid method, Science China, Series A, 51(8) (2008), pp. 1349–1360.CrossRefGoogle Scholar
[5] Chen, C. M., Shi, Z. C. and Hu, H. L., On extrapolation cascadic multigrid method, J. Comput. Math., 29(6) (2011), pp. 684–697.CrossRefGoogle Scholar
[6] Deuflhard, P., Leinen, P. and Yserentant, H., Concepts of an adaptive hierarchical finite element code, IMPACT Comput. Sci. Eng., 1 (1989), pp. 3–35.CrossRefGoogle Scholar
[7] Douglas, J. Jr. and Doupont, T., Galerkin methods for parabolic equations, SIAM J. Numer. Anal., 7 (1970), pp. 575–626.CrossRefGoogle Scholar
[8] Du, Q. and Ming, P. B., Cascadic multigrid methods for parabolic problems, Science in China Series A, 51(8) (2008), pp. 1415–1439.CrossRefGoogle Scholar
[9] Hackbush, W., Fast numerical solution of time-periodic parabolic problem by a multigrid method, SIAM J. Sci. Comput., 2 (1981), pp. 198–206.CrossRefGoogle Scholar
[10] Hackbusch, W., Parabolic multigrid methods, in Computing Methods in Applied Sciences and Engineering, VI, Glowinski, R. and Lions, J. L., eds., North C Holland, Amsterdam: 1984, pp. 189–197.Google Scholar
[11] Hu, H. L., Chen, C. M. and Pan, K. J., Time-extrapolation algorithm (TEA) for linear parabolic problems, J. Comput. Math., 32(2) (2014), pp. 183–194.CrossRefGoogle Scholar
[12] Shi, Z. C. and Xu, X. J., Cascadic multigrid for parabolic problems, J. Comput. Math., 18(5) (2000), pp. 551–560.Google Scholar
[13] Saad, Y., Iterative Method for Sparse Linear Systems, Boston: PWS Publishing Company, 1996.Google Scholar
[14] Shaidurov, V., Some estimates of the rate of convergence for the cascadic conjugate gradient method, Comput. Math. Appl., 31(4-5) (1996), pp. 161–171.CrossRefGoogle Scholar
[15] Strang, G. and Fix, G., An Analysis of the Finite Element Method, Wellesley-Cambridge Press, 1973.Google Scholar
[16] Thomee, V., Galerkin Finite Element Methods for Parabolic Problems, Second edition, New York: Springer-Verlag, 2006.Google Scholar
[17] Wheeler, M., A priori L2error estimates for Galerkin approximations to parabolic partial differential equations, SIAM J. Numer. Anal., 10(4) (1973), pp. 723–759.CrossRefGoogle Scholar