Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Qiao, Zhonghua
Yang, Xuguang
and
Zhang, Yuze
2018.
Mass conservative lattice Boltzmann scheme for a three-dimensional diffuse interface model with Peng-Robinson equation of state.
Physical Review E,
Vol. 98,
Issue. 2,
Yang, Xuguang
and
Wang, Lei
2018.
Lattice Boltzmann study of two-phase hydrocarbon fluids based on Peng–Robinson free energy model.
International Journal of Modern Physics C,
Vol. 29,
Issue. 11,
p.
1850107.
Kou, Jisheng
Sun, Shuyu
and
Wang, Xiuhua
2018.
Linearly Decoupled Energy-Stable Numerical Methods for Multicomponent Two-Phase Compressible Flow.
SIAM Journal on Numerical Analysis,
Vol. 56,
Issue. 6,
p.
3219.
Kou, Jisheng
and
Sun, Shuyu
2018.
Entropy stable modeling of non-isothermal multi-component diffuse-interface two-phase flows with realistic equations of state.
Computer Methods in Applied Mechanics and Engineering,
Vol. 341,
Issue. ,
p.
221.
Chen, Wenbin
Wang, Cheng
Wang, Xiaoming
and
Wise, Steven M.
2019.
Positivity-preserving, energy stable numerical schemes for the Cahn-Hilliard equation with logarithmic potential.
Journal of Computational Physics: X,
Vol. 3,
Issue. ,
p.
100031.
Qiao, Zhonghua
Yang, Xuguang
and
Zhang, Yuze
2019.
Thermodynamic-consistent multiple-relaxation-time lattice Boltzmann equation model for two-phase hydrocarbon fluids with Peng-Robinson equation of state.
International Journal of Heat and Mass Transfer,
Vol. 141,
Issue. ,
p.
1216.
Wang, Xiuhua
Kou, Jisheng
and
Cai, Jianchao
2020.
Stabilized Energy Factorization Approach for Allen–Cahn Equation with Logarithmic Flory–Huggins Potential.
Journal of Scientific Computing,
Vol. 82,
Issue. 2,
Kou, Jisheng
Sun, Shuyu
and
Wang, Xiuhua
2020.
A Novel Energy Factorization Approach for the Diffuse-Interface Model with Peng--Robinson Equation of State.
SIAM Journal on Scientific Computing,
Vol. 42,
Issue. 1,
p.
B30.
Qiao, Zhonghua
Yang, Xuguang
and
Zhang, Yuze
2021.
A Novel Lattice Boltzmann Model for Fourth Order Nonlinear Partial Differential Equations.
Journal of Scientific Computing,
Vol. 87,
Issue. 2,
Wang, Xiuhua
Kou, Jisheng
and
Gao, Huicai
2021.
Linear energy stable and maximum principle preserving semi-implicit scheme for Allen–Cahn equation with double well potential.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 98,
Issue. ,
p.
105766.
Kou, Jisheng
Wang, Xiuhua
Du, Shigui
and
Sun, Shuyu
2022.
An energy stable linear numerical method for thermodynamically consistent modeling of two-phase incompressible flow in porous media.
Journal of Computational Physics,
Vol. 451,
Issue. ,
p.
110854.
Kou, Jisheng
Wang, Xiuhua
and
Du, ShiGui
2022.
Energy Stable and Mass Conservative Numerical Method for Gas Flow in Porous Media with Rock Compressibility.
SIAM Journal on Scientific Computing,
Vol. 44,
Issue. 4,
p.
B938.
Kou, Jisheng
Chen, Huangxin
Du, ShiGui
and
Sun, Shuyu
2023.
An efficient and physically consistent numerical method for the Maxwell–Stefan–Darcy model of two‐phase flow in porous media.
International Journal for Numerical Methods in Engineering,
Vol. 124,
Issue. 3,
p.
546.
Kou, Jisheng
Wang, Xiuhua
Chen, Huangxin
and
Sun, Shuyu
2023.
An efficient bound-preserving and energy stable algorithm for compressible gas flow in porous media.
Journal of Computational Physics,
Vol. 473,
Issue. ,
p.
111751.
Chen, Huangxin
Chen, Yuxiang
and
Kou, Jisheng
2024.
Energy stable finite element approximations of gas flow in poroelastic media.
Computer Methods in Applied Mechanics and Engineering,
Vol. 428,
Issue. ,
p.
117082.
Yan, Yujing
and
Li, Xiaoli
2025.
The linear and efficient structure-preserving method for the thermodynamical consistent model of two-phase flow in porous media with rock compressibility.
Journal of Computational and Applied Mathematics,
Vol. 465,
Issue. ,
p.
116569.
Li, Xiaoli
Yan, Yujing
and
Chen, Huangxin
2025.
A class of high-order physics-preserving schemes for thermodynamically consistent model of incompressible and immiscible two-phase flow in porous media.
Journal of Computational Physics,
Vol. 529,
Issue. ,
p.
113864.
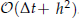 . The numerical results verify the effectiveness of the proposed algorithm and also show good agreement of the numerical solution with laboratory experimental results.
. The numerical results verify the effectiveness of the proposed algorithm and also show good agreement of the numerical solution with laboratory experimental results.

