Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T18:41:26.273Z Has data issue: false hasContentIssue false
  • English
  • Français

A High-Accuracy Mechanical Quadrature Method for Solving the Axisymmetric Poisson's Equation

Part of: Integral equations, integral transforms Partial differential equations, boundary value problems

Published online by Cambridge University Press:  09 January 2017

Hu Li  and
Jin Huang
Hu Li*
Affiliation:
School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China
Jin Huang
Affiliation:
School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China
*
*Corresponding author. Email:[email protected] (H. Li)
Get access

Abstract

In this article, we consider the numerical solution for Poisson's equation in axisymmetric geometry. When the boundary condition and source term are axisymmetric, the problem reduces to solving Poisson's equation in cylindrical coordinates in the two-dimensional (r,z) region of the original three-dimensional domain S. Hence, the original boundary value problem is reduced to a two-dimensional one. To make use of the Mechanical quadrature method (MQM), it is necessary to calculate a particular solution, which can be subtracted off, so that MQM can be used to solve the resulting Laplace problem, which possesses high accuracy order 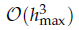and low computing complexities. Moreover, the multivariate asymptotic error expansion of MQM accompanied with 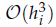for all mesh widths hi is got. Hence, once discrete equations with coarse meshes are solved in parallel, the higher accuracy order of numerical approximations can be at least 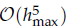by the splitting extrapolation algorithm (SEA). Meanwhile, a posteriori asymptotic error estimate is derived, which can be used to construct self-adaptive algorithms. The numerical examples support our theoretical analysis.

Keywords

Mechanical quadrature methodsplitting extrapolation algorithmPoisson's equationa posteriori estimate

MSC classification

Secondary: 65N38: Boundary element methods 65R20: Integral equations
Type
Research Article
Information
Advances in Applied Mathematics and Mechanics , Volume 9 , Issue 2 , April 2017 , pp. 393 - 406
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Temem, R., NavierCStokes Equations, Theory and Numerical Analysis, Elsevier, New York, 1984.Google Scholar
[2] Fletcher, C. A. J., Computational Techniques for Fluid Dynamics, Springer, New York, 1991.Google Scholar
[3] Pierce, A. D., Acoustics: An Introduction to Its Physical Principles and Applications, Acoustical Society of America, Woodbury, New York, 1989.Google Scholar
[4] Jaluria, Y. and Torrance, K. E., Computational Heat Transfer, New York, 2003.Google Scholar
[5] Harari, I. and Turkel, E., Accurate finite difference methods for time-harmonic wave propagation, J. Comput. Phys., 119 (1995), pp. 252–270.Google Scholar
[6] Schumann, U. and Sweet, R. A., Fast Fourier transforms for direct solution of Poisson's equation with staggered boundary conditions, J. Comput. Phys., 75 (1998), pp. 123–127.Google Scholar
[7] Mckenney, A., Greengard, L. and Mayo, A., A fast Poisson solver for complex geometries, J. Comput. Phys., 118 (1995), pp. 348–355.Google Scholar
[8] Schumann, U. and Sweet, R., A direct method for the solution of Poisson equation with Neumann boundary conditions on a staggered grid of arbitrary sizes, J. Comput. Phys., 20 (1976), pp. 171–182.Google Scholar
[9] Buzbee, B. L., Golub, G. H. and Nielson, C. W., On direct methods for solving Poisson's equations, SIAM J. Numer. Anal., 7 (1970), pp. 627–656.Google Scholar
[10] Swarztrauber, P. N. and Sweet, R. A., The Fourier and cyclic reduction methods for solving Poisson's equation, in: Schetz, J. A., Fuhs, A. E. (Eds.), Hand book of Fluid Dynamics and Fluid Machinery, John Wiley and Sons, New York, 1996.Google Scholar
[11] Huang, J. and Lu, T., Splitting Extrapolations for solving boundary integral equations of linear elasticity dirichlet problems on polygons by mechanical quadrature methods, J. Comput. Math., 1 (2006), pp. 9–18.Google Scholar
[12] Lin, Q. and Lu, T., Splitting Extrapolation for multidimensional problems, J. Comput. Math., 1 (1983), pp. 45–51.Google Scholar
[13] Lin, C. B., Lu, T. and Shih, T. M., The Splitting Extrapolation Method, World Scientific, Singapore, 1995.Google Scholar
[14] Lu, T. and Huang, J., Quadrature methods with high accuarcy and Extrapolation for solving boundary integral equations of first-kind, J. Math. Num. Sinica, 1 (2000), pp. 59–72.Google Scholar
[15] Zhu, R, Huang, J. and Tao, L., Mechanical quadrature methods and their splitting extrapolations for solving boundary integral equations of axisymmetric laplace mixed boundary value problems, Eng. Anal. Boundary Element, 30 (2006), pp. 391–398.Google Scholar
[16] Huang, J., Lu, T. and Li, Z. C., The mechanical quadrature methods and their splitting extrapolation for boundary integral equations of first kind on open contours, Appl. Numer. Math., 59 (2009), pp. 8–22.Google Scholar
[17] Sidi, A., A new variable transformation for numerical integration, in integration IV. Frankfurt: Birkhaurer Verlag, 1993.Google Scholar
[18] Sidi, A. and Israrli, M., Quadrature methods for periodic singular fredholm integral equations, J. Sci. Comput., 3 (1988), pp. 201–231.Google Scholar
[19] Sloan, I. H. and Spence, A., The galerkin method for integral equations of the first kind with logarithmic kernel, IMA J. Numer. Anal., V (1988), pp. 105–122.Google Scholar
[20] Yi, Y., The collocation method for the first kind with boundary integral equation on polygonal region, Math. Comput., 54 (1990), pp. 139–154.Google Scholar
[21] Yi, Y. and Sloan, I., On integral equations of the first kind with logarithmic kernel, J. Integral Equations Appl., 1 (1988), pp. 549–579.Google Scholar
[22] Huang, J. and Wang, Z., Extraplotion algorithms for solving mixed boundary integral equations of the Helmholz equation by Mechanical quadrature methods, SIAM J. Sci. Comput., 31 (2009), pp. 4115–4129.Google Scholar
[23] Atkinson, K., The Numerical Solution of Integral Equations of the Second Kind, Cambridge University Press, Cambridge, 1977.Google Scholar
[24] Davis, P., Methods of Numerical Integration, Second, Academic Press, New York, 1984.Google Scholar
[25] Cai, H. and Xu, Y., A fast Fourier-Galerkin method for solving singular boundary integral equations, SIAM J. Numer. Anal., 46 (2008), pp. 1965–1984.Google Scholar
[26] Li, H., Finite element analysis for the axisymmetric Laplace operator on polygonal domains, J. Comput. Appl. Math., 235 (2011), pp. 5155–5176.Google Scholar