Article contents
Error Analysis for a Non-Monotone FEM for a Singularly Perturbed Problem with Two Small Parameters
Published online by Cambridge University Press: 10 March 2015
Abstract
In this paper, we consider a singularly perturbed convection-diffusion problem. The problem involves two small parameters that gives rise to two boundary layers at two endpoints of the domain. For this problem, a non-monotone finite element methods is used. A priori error bound in the maximum norm is obtained. Based on the a priori error bound, we show that there exists Bakhvalov-type mesh that gives optimal error bound of 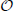 (N−2) which is robust with respect to the two perturbation parameters. Numerical results are given that confirm the theoretical result.
(N−2) which is robust with respect to the two perturbation parameters. Numerical results are given that confirm the theoretical result.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Global-Science Press 2015
References
- 1
- Cited by


