Published online by Cambridge University Press: 27 April 2015
Parametrized families of PDEs arise in various contexts such as inverse problems, control and optimization, risk assessment, and uncertainty quantification. In most of these applications, the number of parameters is large or perhaps even infinite. Thus, the development of numerical methods for these parametric problems is faced with the possible curse of dimensionality. This article is directed at (i) identifying and understanding which properties of parametric equations allow one to avoid this curse and (ii) developing and analysing effective numerical methods which fully exploit these properties and, in turn, are immune to the growth in dimensionality.
Part I of this article studies the smoothness and approximability of the solution map, that is, the map  $a\mapsto u(a)$, where
$a\mapsto u(a)$, where  $a$ is the parameter value and
$a$ is the parameter value and 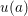 $u(a)$ is the corresponding solution to the PDE. It is shown that for many relevant parametric PDEs, the parametric smoothness of this map is typically holomorphic and also highly anisotropic, in that the relevant parameters are of widely varying importance in describing the solution. These two properties are then exploited to establish convergence rates of
$u(a)$ is the corresponding solution to the PDE. It is shown that for many relevant parametric PDEs, the parametric smoothness of this map is typically holomorphic and also highly anisotropic, in that the relevant parameters are of widely varying importance in describing the solution. These two properties are then exploited to establish convergence rates of  $n$-term approximations to the solution map, for which each term is separable in the parametric and physical variables. These results reveal that, at least on a theoretical level, the solution map can be well approximated by discretizations of moderate complexity, thereby showing how the curse of dimensionality is broken. This theoretical analysis is carried out through concepts of approximation theory such as best
$n$-term approximations to the solution map, for which each term is separable in the parametric and physical variables. These results reveal that, at least on a theoretical level, the solution map can be well approximated by discretizations of moderate complexity, thereby showing how the curse of dimensionality is broken. This theoretical analysis is carried out through concepts of approximation theory such as best  $n$-term approximation, sparsity, and
$n$-term approximation, sparsity, and  $n$-widths. These notions determine a priori the best possible performance of numerical methods and thus serve as a benchmark for concrete algorithms.
$n$-widths. These notions determine a priori the best possible performance of numerical methods and thus serve as a benchmark for concrete algorithms.
Part II of this article turns to the development of numerical algorithms based on the theoretically established sparse separable approximations. The numerical methods studied fall into two general categories. The first uses polynomial expansions in terms of the parameters to approximate the solution map. The second one searches for suitable low-dimensional spaces for simultaneously approximating all members of the parametric family. The numerical implementation of these approaches is carried out through adaptive and greedy algorithms. An a priori analysis of the performance of these algorithms establishes how well they meet the theoretical benchmarks.