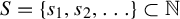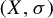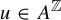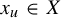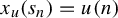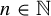We present a streamlined proof of a result essentially presented by the author in [Some counterexamples in topological dynamics. Ergod. Th. & Dynam. Sys. 28(4) (2008), 1291–1322], namely that for every set 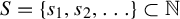 $S = \{s_1, s_2, \ldots \} \subset \mathbb {N}$ of zero Banach density and finite set A, there exists a minimal zero-entropy subshift
$S = \{s_1, s_2, \ldots \} \subset \mathbb {N}$ of zero Banach density and finite set A, there exists a minimal zero-entropy subshift 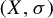 $(X, \sigma )$ so that for every sequence
$(X, \sigma )$ so that for every sequence 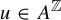 $u \in A^{\mathbb {Z}}$, there is
$u \in A^{\mathbb {Z}}$, there is 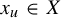 $x_u \in X$ with
$x_u \in X$ with 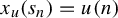 $x_u(s_n) = u(n)$ for all
$x_u(s_n) = u(n)$ for all 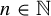 $n \in \mathbb {N}$. Informally, minimal deterministic sequences can achieve completely arbitrary behavior upon restriction to a set of zero Banach density. As a corollary, this provides counterexamples to the polynomial Sarnak conjecture reported by Eisner [A polynomial version of Sarnak’s conjecture. C. R. Math. Acad. Sci. Paris 353(7) (2015), 569–572] which are significantly more general than some recently provided by Kanigowski, Lemańczyk and Radziwiłł [Prime number theorem for analytic skew products. Ann. of Math. (2) 199 (2024), 591–705] and by Lian and Shi [A counter-example for polynomial version of Sarnak’s conjecture. Adv. Math. 384 (2021), Paper no. 107765] and shows that no similar result can hold under only the assumptions of minimality and zero entropy.
$n \in \mathbb {N}$. Informally, minimal deterministic sequences can achieve completely arbitrary behavior upon restriction to a set of zero Banach density. As a corollary, this provides counterexamples to the polynomial Sarnak conjecture reported by Eisner [A polynomial version of Sarnak’s conjecture. C. R. Math. Acad. Sci. Paris 353(7) (2015), 569–572] which are significantly more general than some recently provided by Kanigowski, Lemańczyk and Radziwiłł [Prime number theorem for analytic skew products. Ann. of Math. (2) 199 (2024), 591–705] and by Lian and Shi [A counter-example for polynomial version of Sarnak’s conjecture. Adv. Math. 384 (2021), Paper no. 107765] and shows that no similar result can hold under only the assumptions of minimality and zero entropy.