1 results
Phase transition in the random triangle model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1101-1115
- Print publication:
- December 1999
-
- Article
- Export citation
-
The random triangle model was recently introduced as a random graph model that captures the property of transitivity that is often found in social networks, i.e. the property that given that two vertices are second neighbors, they are more likely to be neighbors. For parameters p ∊ [0,1] and q ≥ 1, and a finite graph G = (V, E), it assigns to elements η of {0,1}E probabilities which are proportional to
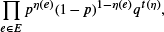where t(η) is the number of triangles in the open subgraph. In this paper the behavior of the random triangle model on the two-dimensional triangular lattice is studied. By mapping the system onto an Ising model with external field on the hexagonal lattice, it is shown that phase transition occurs if and only if p = (q−1)−2/3 and q > qc for a critical value qc which turns out to equal 
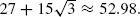It is furthermore demonstrated that phase transition cannot occur unless p = pc(q), the critical value for percolation of open edges for given q. This implies that for q ≥ qc, pc(q) = (q−1)−2/3.
It is furthermore demonstrated that phase transition cannot occur unless 