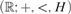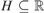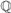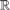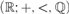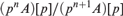In this note, we construct a distal expansion for the structure $$\left( {; + , < ,H} \right)$$, where $H \subseteq $ is a dense $Q$-vector space basis of $R$ (a so-called Hamel basis). Our construction is also an expansion of the dense pair $\left( {; + , < ,} \right)$ and has full quantifier elimination in a natural language.

An equation to compute the dp-rank of any abelian group is given. It is also shown that its dp-rank, or more generally that of any one-based group, agrees with its Vapnik–Chervonenkis density. Furthermore, strong abelian groups are characterised to be precisely those abelian groups A such that there are only finitely many primes p such that the group A / pA is infinite and for every prime p, there are only finitely many natural numbers n such that $\left( {p^n A} \right)[p]/\left( {p^{n + 1} A} \right)[p]$ is infinite.

Finally, it is shown that an infinite stable field of finite dp-rank is algebraically closed.

This paper has two parts. In the first one, we prove that an invariant dp-minimal type is either finitely satisfiable or definable. We also prove that a definable version of the (p,q)-theorem holds in dp-minimal theories of small or medium directionality.

In the second part, we study dp-rank in dp-minimal theories and show that it enjoys many nice properties. It is continuous, definable in families and it can be characterised geometrically with no mention of indiscernible sequences. In particular, if the structure expands a divisible ordered abelian group, then dp-rank coincides with the dimension coming from the order.