We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Consider an analytic Hamiltonian system near its analytic invariant torus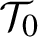 
$\mathcal T_0$
carrying zero frequency. We assume that the Birkhoff normal form of the Hamiltonian at 
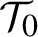$\mathcal T_0$
is convergent and has a particular form: it is an analytic function of its non-degenerate quadratic part. We prove that in this case there is an analytic canonical transformation—not just a formal power series—bringing the Hamiltonian into its Birkhoff normal form.
