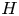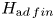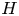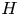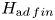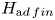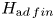We consider the adjoint representation of a Hopf algebra $H$ focusing on the locally finite part, $H_{{\textrm ad\,fin}}$, defined as the sum of all finite-dimensional subrepresentations. For virtually cocommutative $H$ 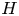(i.e., $H$ 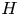is finitely generated as module over a cocommutative Hopf subalgebra), we show that $H_{{\textrm ad\,fin}}$ 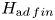is a Hopf subalgebra of $H$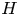. This is a consequence of the fact, proved here, that locally finite parts yield a tensor functor on the module category of any virtually pointed Hopf algebra. For general Hopf algebras, $H_{{\textrm ad\,fin}}$ 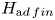is shown to be a left coideal subalgebra. We also prove a version of Dietzmann's Lemma from group theory for Hopf algebras.

In this article, we give an explicit formula to compute the non abelian twisted sign-determined Reidemeister torsion of the exterior of a fibered knot in terms of its monodromy. As an application, we give explicit formulae for the non abelian Reidemeister torsion of torus knots and of the figure eight knot.

Exterior powers of the adjoint representation of a complex semisimple Lie algebra are decomposed into irreducible representations, to varying degrees of satisfaction.