Let $E$ and $D$ be open subsets of $\mathbb{R}^{n+1}$ such that $\overline{D}$ is a compact subset of $E$, and let $v$ be a supertemperature on $E$. We call a temperature $u$ on $D$extendable by$v$ if there is a supertemperature $w$ on $E$ such that $w=u$ on $D$ and $w=v$ on $E\backslash \overline{D}$. Such a temperature need not be a thermic minorant of $v$ on $D$. We show that either there is a unique temperature extendable by $v$, or there are infinitely many. Examples of temperatures extendable by $v$ include the greatest thermic minorant $GM_{v}^{D}$ of $v$ on $D$, and the Perron–Wiener–Brelot solution of the Dirichlet problem $S\!_{v}^{D}$ on $D$ with boundary values the restriction of $v$ to $\unicode[STIX]{x2202}D$. In the case where these two examples are distinct, we give a formula for producing infinitely many more. Clearly $GM_{v}^{D}$ is the greatest extendable thermic minorant, but we also prove that there is a least one, which is not necessarily equal to $S\!_{v}^{D}$.

We solve a problem posed by Blasco, Bonilla and Grosse-Erdmann in 2010 by constructing a harmonic function on ℝN, that is frequently hypercyclic with respect to the partial differentiation operator ∂/∂xk and which has a minimal growth rate in terms of the average L2-norm on spheres of radius r > 0 as r → ∞.

Let $u$ be a supertemperature on an open set $E$, and let $v$ be a related temperature on an open subset $D$ of $E$. For example, $v$ could be the greatest thermic minorant of $u$ on $D$, if it exists. Putting $w=u$ on $E\setminus D$ and $w=v$ on $D$, we investigate whether $w$, or its lower semicontinuous smoothing, is a supertemperature on $E$. We also give a representation of the greatest thermic minorant on $E$, if it exists, in terms of PWB solutions on an expanding sequence of open subsets of $E$ with union $E$.  In addition, in the case of a nonnegative supertemperature, we prove inequalities that relate reductions to Dirichlet solutions. We also prove that the value of any reduction at a given time depends only on earlier times.

We show that the null limit hypothesis, in the definition of a barrier, can be relaxed for normal boundary points that satisfy a mild additional condition. We also give a simple necessary and sufficient condition for the regularity of semi-singular boundary points.

By applying Wei, Li and Wu's notion (given in ‘Generalizations of the uniformization theorem and Bochner's method in p-harmonic geometry’, Comm. Math. Anal. Conf., vol. 01, 2008, pp. 46–68) and method (given in ‘Sharp estimates on -harmonic functions with applications in biharmonic maps, preprint) and by modifying the proof of a general inequality given by Chen in ‘On isometric minimal immersion from warped products into space forms’ (Proc. Edinb. Math. Soc., vol. 45, 2002, pp. 579–587), we establish some simple relations between geometric estimates (the mean curvature of an isometric immersion of a warped product and sectional curvatures of an ambient m-manifold 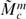bounded from above by a non-positive number c) and analytic estimates (the growth of the warping function). We find a dichotomy between constancy and ‘infinity’ of the warping functions on complete non-compact Riemannian manifolds for an appropriate isometric immersion. Several applications of our growth estimates are also presented. In particular, we prove that if f is an Lq function on a complete non-compact Riemannian manifold N1 for some q > 1, then for any Riemannian manifold N2 the warped product N1 ×fN2 does not admit a minimal immersion into any non-positively curved Riemannian manifold. We also show that both the geometric curvature estimates and the analytic function growth estimates in this paper are sharp.

The characterization by weighted Lipschitz continuity is given for the Bloch space on the unit ball of $\mathbb{R}^n$. Similar results are obtained for little Bloch and Besov spaces.