1 results
Precise large deviations for a multidimensional risk model with regression dependence structure
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 448-457
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In this paper, we consider a nonstandard multidimensional risk model, in which the claim sizes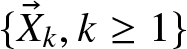
$\{\vec{X}_k, k\ge 1\}$ form an independent and identically distributed random vector sequence with dependent components. By assuming that there exists the regression dependence structure between inter-arrival time and the claim-size vectors, we extend the regression dependence to a more practical multidimensional risk model. For the univariate marginal distributions of claim vectors with consistently varying tails, we obtain the precise large deviation formulas for the multidimensional risk model with the regression size-dependent structure.
