1 results
A transport process on graphs and its limiting distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 341-357
- Print publication:
- March 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
Given a finite strongly connected directed graph
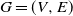$G=(V, E)$
, we study a Markov chain taking values on the space of probability measures on V. The chain, motivated by biological applications in the context of stochastic population dynamics, is characterized by transitions between states that respect the structure superimposed by E: mass (probability) can only be moved between neighbors in G. We provide conditions for the ergodicity of the chain. In a simple, symmetric case, we fully characterize the invariant probability.
