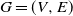1. Introduction and motivation
1.1. Description
Let
![]() $G=(V, E)$
be a strongly connected directed graph without loops. This means that G is a graph with directed edges such that for any two different vertices there exists a directed path joining them. We endow G with a probability vector indexed by E,
$G=(V, E)$
be a strongly connected directed graph without loops. This means that G is a graph with directed edges such that for any two different vertices there exists a directed path joining them. We endow G with a probability vector indexed by E,
![]() $\textbf{p}\;:\!=\; (p_{ij}\colon ij \in E)$
. This means that
$\textbf{p}\;:\!=\; (p_{ij}\colon ij \in E)$
. This means that
![]() $p_{ij }>0$
if and only if
$p_{ij }>0$
if and only if
![]() $ij \in E$
, and
$ij \in E$
, and
![]() $\sum_{ij}p_{ij}=1$
. Hereafter, we refer to a pair
$\sum_{ij}p_{ij}=1$
. Hereafter, we refer to a pair
![]() $(G, {\bf p})$
as a transport scheme on G.
$(G, {\bf p})$
as a transport scheme on G.
Assume that
![]() $\vert V \vert = m \ge 2$
. Let
$\vert V \vert = m \ge 2$
. Let
![]() $\Delta_V$
be the set of probability measures on V. We identify
$\Delta_V$
be the set of probability measures on V. We identify
![]() $\Delta_V$
with the
$\Delta_V$
with the
![]() $(m-1)$
-dimensional simplex, and consequently we endow
$(m-1)$
-dimensional simplex, and consequently we endow
![]() $\Delta_V$
with the Euclidean topology inherited from
$\Delta_V$
with the Euclidean topology inherited from
![]() $\mathbb{R}^{m-1}$
. Observe that since
$\mathbb{R}^{m-1}$
. Observe that since
![]() $\Delta_V$
is finite-dimensional, this topology and the weak topology of probability measures coincide in our case. In many situations we freely identify V with the set
$\Delta_V$
is finite-dimensional, this topology and the weak topology of probability measures coincide in our case. In many situations we freely identify V with the set
![]() $[1,\ldots, m]$
, without further mention of this convention. We use the notation
$[1,\ldots, m]$
, without further mention of this convention. We use the notation
![]() $\textrm{Leb}_{m-1}$
to denote the Lebesgue measure on
$\textrm{Leb}_{m-1}$
to denote the Lebesgue measure on
![]() $\Delta_V$
. The space of continuous (resp. bounded Borel) functions on
$\Delta_V$
. The space of continuous (resp. bounded Borel) functions on
![]() $\Delta_V$
will be denoted by
$\Delta_V$
will be denoted by
![]() $\mathcal{C}(\Delta_V)$
(resp.
$\mathcal{C}(\Delta_V)$
(resp.
![]() $\mathcal{B}(\Delta_V)$
).
$\mathcal{B}(\Delta_V)$
).
Given
in this paper we aim to study the following dynamics. For
![]() $n \ge 0$
, given
$n \ge 0$
, given
![]() $\mu_n \in \Delta_V$
, choose an edge
$\mu_n \in \Delta_V$
, choose an edge
![]() $i_{n+1}j_{n+1}\;:\!=\; e_{n+1} \in E$
with probability
$i_{n+1}j_{n+1}\;:\!=\; e_{n+1} \in E$
with probability
![]() $p_{e_{n+1}}$
and independently draw
$p_{e_{n+1}}$
and independently draw
![]() $U_{n+1}\sim \operatorname{Uniform}(0,1)$
. Define
$U_{n+1}\sim \operatorname{Uniform}(0,1)$
. Define
![]() $\mu_{n+1}$
as
$\mu_{n+1}$
as
 \begin{align}\mu_{n+1}^{(k)}& = \mu_{n}^{(k)}, \quad k \neq i_{n+1},\, j_{n+1}, \nonumber \\[5pt] \mu_{n+1}^{(i_{n+1})}&= (1-U_{n+1})\mu_{n}^{(i_{n+1})}, \\[5pt] \mu_{n+1}^{(j_{n+1})}&= \mu_{n}^{(j_{n+1})}+ U_{n+1} \mu_{n}^{(i_{n+1})}\nonumber \end{align}
\begin{align}\mu_{n+1}^{(k)}& = \mu_{n}^{(k)}, \quad k \neq i_{n+1},\, j_{n+1}, \nonumber \\[5pt] \mu_{n+1}^{(i_{n+1})}&= (1-U_{n+1})\mu_{n}^{(i_{n+1})}, \\[5pt] \mu_{n+1}^{(j_{n+1})}&= \mu_{n}^{(j_{n+1})}+ U_{n+1} \mu_{n}^{(i_{n+1})}\nonumber \end{align}
In words: we move to
![]() $j_{n+1}$
a chunk of size uniformly chosen from the heap at vertex
$j_{n+1}$
a chunk of size uniformly chosen from the heap at vertex
![]() $i_{n+1}$
.
$i_{n+1}$
.
From now on, we refer to the process
![]() $(\mu_n\colon n \ge 0)$
as the transport process on
$(\mu_n\colon n \ge 0)$
as the transport process on
![]() $(G, {\bf p})$
.
$(G, {\bf p})$
.
The description above has many points in common with other mass transport processes on graphs. For example, under the condition of symmetric weights (i.e.
![]() $p_{ij}=p_{ji}$
), the transport process (or an easily derivable continuous-time version of it) can be regarded as a smooth version of the averaging process (see [Reference Aldous and Lanoue1]), in that the expectations obey the same linear dynamics, up to a constant velocity factor (see the closing remarks at the end of this paper). It is known, however, that in the averaging process the limit distribution is the point mass at the uniform distribution, a situation that certainly does not hold in our model. Also, in [Reference Smith14], Smith considered general Gibbs samplers on graphs based on moves between adjacent vertices, and studied rates of convergence to the invariant measure. In his case, this invariant measure is always uniformly distributed. As the reader will see, the relevant distribution in our model (at least in the cases we study here) comes from the Dirichlet family. In [Reference Smith15], Smith studied convergence rates of a sampler with mass exchange on the set of vertices of the complete graph; although his model is strongly tuned to deal with this particular structure, he suggests that a slight modification to his model would yield the Dirichlet distribution as the limiting law. In contrast, our model allows for general connected graphs as the underlying structure for the allowed moves, and we are more interested in fundamental ergodic properties than estimates of convergence rates. In any case, as far as we know, the transport process, as described above, has not been studied in the previous literature.
$p_{ij}=p_{ji}$
), the transport process (or an easily derivable continuous-time version of it) can be regarded as a smooth version of the averaging process (see [Reference Aldous and Lanoue1]), in that the expectations obey the same linear dynamics, up to a constant velocity factor (see the closing remarks at the end of this paper). It is known, however, that in the averaging process the limit distribution is the point mass at the uniform distribution, a situation that certainly does not hold in our model. Also, in [Reference Smith14], Smith considered general Gibbs samplers on graphs based on moves between adjacent vertices, and studied rates of convergence to the invariant measure. In his case, this invariant measure is always uniformly distributed. As the reader will see, the relevant distribution in our model (at least in the cases we study here) comes from the Dirichlet family. In [Reference Smith15], Smith studied convergence rates of a sampler with mass exchange on the set of vertices of the complete graph; although his model is strongly tuned to deal with this particular structure, he suggests that a slight modification to his model would yield the Dirichlet distribution as the limiting law. In contrast, our model allows for general connected graphs as the underlying structure for the allowed moves, and we are more interested in fundamental ergodic properties than estimates of convergence rates. In any case, as far as we know, the transport process, as described above, has not been studied in the previous literature.
1.2. Our results
Obviously, the transport process is a
![]() $\Delta_V$
-valued Markov chain. Let
$\Delta_V$
-valued Markov chain. Let
![]() $\mathbb{P}_\mu$
,
$\mathbb{P}_\mu$
,
![]() $\mathbb{E}_\mu$
be the associated probability measure and expectation operator, respectively, when the chain is started from
$\mathbb{E}_\mu$
be the associated probability measure and expectation operator, respectively, when the chain is started from
![]() $\mu \in \Delta_V$
. Let P be the transition kernel of the chain, that is,
$\mu \in \Delta_V$
. Let P be the transition kernel of the chain, that is,
![]() $P\colon \mathcal{B}(\Delta_V) \mapsto \mathcal{B}(\Delta_V)$
is the operator given by
$P\colon \mathcal{B}(\Delta_V) \mapsto \mathcal{B}(\Delta_V)$
is the operator given by
As usual, for
![]() $x \in \Delta_V$
, we adopt the notation
$x \in \Delta_V$
, we adopt the notation
![]() $P(x, \cdot)$
to denote the probability measure on
$P(x, \cdot)$
to denote the probability measure on
![]() $\Delta_V$
given by
$\Delta_V$
given by
![]() ${\mathcal{B}(\Delta_V) \ni A \mapsto P\textbf{1}_A (x)}$
. Let
${\mathcal{B}(\Delta_V) \ni A \mapsto P\textbf{1}_A (x)}$
. Let
![]() $\mathcal{P}\;:\!=\; \mathcal{P} (\Delta_V)$
be the space of probability measures on
$\mathcal{P}\;:\!=\; \mathcal{P} (\Delta_V)$
be the space of probability measures on
![]() $\mathcal{B}(\Delta_V)$
. As is customary, we consider the action of the transition kernel P acting on
$\mathcal{B}(\Delta_V)$
. As is customary, we consider the action of the transition kernel P acting on
![]() $\mathcal{P}$
from the right by definition: for
$\mathcal{P}$
from the right by definition: for
![]() $M \in \mathcal{P}$
, MP is the unique element
$M \in \mathcal{P}$
, MP is the unique element
![]() $ M' \in \mathcal{P}$
such that for every
$ M' \in \mathcal{P}$
such that for every
![]() $F \in \mathcal{B} (\Delta_V)$
,
$F \in \mathcal{B} (\Delta_V)$
,
Recall that a probability measure M is said to be invariant or stationary for P if
![]() $MP=M$
, and it is called a limiting distribution if for some initial probability measure
$MP=M$
, and it is called a limiting distribution if for some initial probability measure
![]() $\pi$
we have
$\pi$
we have
![]() $\pi P^n \to M$
weakly as
$\pi P^n \to M$
weakly as
![]() $n \to \infty$
. In this case we say that
$n \to \infty$
. In this case we say that
![]() $\pi$
is in the basin of attraction of P. A chain (or its transition operator) is ergodic if it admits a unique invariant distribution whose basin of attraction is the whole of
$\pi$
is in the basin of attraction of P. A chain (or its transition operator) is ergodic if it admits a unique invariant distribution whose basin of attraction is the whole of
![]() $\mathcal{P}$
.
$\mathcal{P}$
.
In this article we will focus on the problem of existence, uniqueness, and (at least in a simple case) the identification of the invariant distributions for P. The next results, whose proofs will be provided in the following pages, are the highlights of this article.
Theorem 1. Assume
![]() ${\vert V \vert} \ge 2$
. Then P is ergodic, and its unique invariant measure is absolutely continuous with respect to Lebesgue measure.
${\vert V \vert} \ge 2$
. Then P is ergodic, and its unique invariant measure is absolutely continuous with respect to Lebesgue measure.
Theorem 2. Assume that
![]() ${\vert V \vert}=2$
. Let M be the unique stationary distribution of P. If
${\vert V \vert}=2$
. Let M be the unique stationary distribution of P. If
![]() $(X, 1-X)$
is distributed as M, then X has the Beta distribution
$(X, 1-X)$
is distributed as M, then X has the Beta distribution
![]() $\operatorname{Beta}(p_{21}, p_{12})$
.
$\operatorname{Beta}(p_{21}, p_{12})$
.
Theorem 3. Assume that
![]() ${\vert V \vert} \ge 2$
, and moreover assume that
${\vert V \vert} \ge 2$
, and moreover assume that
![]() $p_{ij}=p_{ji}$
for every
$p_{ij}=p_{ji}$
for every
![]() $ij \in E$
. Then the unique stationary distribution is given by the Dirichlet distribution with concentration parameter
$ij \in E$
. Then the unique stationary distribution is given by the Dirichlet distribution with concentration parameter
![]() $1/2$
.
$1/2$
.
1.3. A biological motivation
Although in this paper our presentation can be followed without mention of any particular application, some words about the motivation to study the transport process are in order. Indeed, the transport process arises as a first step in the agenda of characterizing the properties of a larger process regarding stochastic population dynamics. For example, consider a simple Lotka–Volterra model driven by Lévy noise, namely
Here
![]() $B \in \mathbb{R}^n$
is a constant vector representing the rates of increase or decrease of the species,
$B \in \mathbb{R}^n$
is a constant vector representing the rates of increase or decrease of the species,
![]() $A, \Sigma$
are constant
$A, \Sigma$
are constant
![]() $n \times n$
real matrices, W is a standard n-dimensional Brownian motion,
$n \times n$
real matrices, W is a standard n-dimensional Brownian motion,
![]() $L\colon \mathbb{R}^n \times \mathbb{R}^n \mapsto \mathbb{R}^n$
is a measurable, reasonable function, and
$L\colon \mathbb{R}^n \times \mathbb{R}^n \mapsto \mathbb{R}^n$
is a measurable, reasonable function, and
![]() $\tilde N$
is a compensated Poisson measure of intensity measure
$\tilde N$
is a compensated Poisson measure of intensity measure
![]() $\textrm{d}t\nu (\textrm{d}z)$
, where
$\textrm{d}t\nu (\textrm{d}z)$
, where
![]() $\nu$
is a finite measure. Stochastic systems such as (2) have been previously studied in the literature (see e.g. [Reference Bao, Mao, Yin and Yuan2], [Reference Liu and Wang9], and more recently [Reference Videla18]). Under certain conditions on
$\nu$
is a finite measure. Stochastic systems such as (2) have been previously studied in the literature (see e.g. [Reference Bao, Mao, Yin and Yuan2], [Reference Liu and Wang9], and more recently [Reference Videla18]). Under certain conditions on
![]() $\tilde N$
, it can be proved that the process X is an
$\tilde N$
, it can be proved that the process X is an
![]() $\mathbb{R}^n$
-valued right-continuous strong Markov–Feller process, with the vector
$\mathbb{R}^n$
-valued right-continuous strong Markov–Feller process, with the vector
![]() $X_t$
usually interpreted as the vector of abundances of the n species at time t. Consider the case where the process is intended to model a simple ecological network with one predator (species 1) and
$X_t$
usually interpreted as the vector of abundances of the n species at time t. Consider the case where the process is intended to model a simple ecological network with one predator (species 1) and
![]() $m \ge 2$
prey species (species 2 through
$m \ge 2$
prey species (species 2 through
![]() $m+1$
). In this situation the constant matrix A, called the interaction matrix, has components
$m+1$
). In this situation the constant matrix A, called the interaction matrix, has components
![]() $A_{1,j}>0$
and
$A_{1,j}>0$
and
![]() $A_{j,1}<0$
for
$A_{j,1}<0$
for
![]() $j=2, 3, \ldots, m+1$
, and these values are interpreted as the average rate of increase (resp. decrease) of the fitness of the predator per encounter with prey j (resp. the fitness of the prey species j per encounter with the predator). Now it has been observed that some predators are able to modify their foraging strategies in accordance with the density of prey species. When the prey species j, say, is becoming less abundant than species k, the predator tends to change its hunting behavior, becoming increasingly specialized in hunting more of k and less of j. In turn, this shift in the interest of the predator modifies the fitness of the species j and k. This phenomenon, known in the ecology literature as prey-switching behavior (PSB: see e.g. [Reference Murdoch10]), has been studied previously in the mathematical biology literature; see [Reference Piltz, Porter and Maini11] and [Reference Teramoto, Kawasaki and Shigesada16] for a formulation based on deterministic dynamical systems, and, in a simple stochastic setting, [Reference Hening, Nguyen and Schreiber7]. To introduce this effect into our model, we impose dynamics on the interaction matrix, thus obtaining a new matrix-valued process
$j=2, 3, \ldots, m+1$
, and these values are interpreted as the average rate of increase (resp. decrease) of the fitness of the predator per encounter with prey j (resp. the fitness of the prey species j per encounter with the predator). Now it has been observed that some predators are able to modify their foraging strategies in accordance with the density of prey species. When the prey species j, say, is becoming less abundant than species k, the predator tends to change its hunting behavior, becoming increasingly specialized in hunting more of k and less of j. In turn, this shift in the interest of the predator modifies the fitness of the species j and k. This phenomenon, known in the ecology literature as prey-switching behavior (PSB: see e.g. [Reference Murdoch10]), has been studied previously in the mathematical biology literature; see [Reference Piltz, Porter and Maini11] and [Reference Teramoto, Kawasaki and Shigesada16] for a formulation based on deterministic dynamical systems, and, in a simple stochastic setting, [Reference Hening, Nguyen and Schreiber7]. To introduce this effect into our model, we impose dynamics on the interaction matrix, thus obtaining a new matrix-valued process
![]() $A_t$
. This means that the interaction matrix, which was a constant in the model (2), now becomes a dynamic object. Thus the fundamental object of study is now the pair
$A_t$
. This means that the interaction matrix, which was a constant in the model (2), now becomes a dynamic object. Thus the fundamental object of study is now the pair
![]() $\Xi_t\;:\!=\; (X_t, A_t)$
whose joint dynamics is governed by
$\Xi_t\;:\!=\; (X_t, A_t)$
whose joint dynamics is governed by
 \begin{align*} {\textrm{d}} X_{t}& =\textrm{diag} (X_{t}) \biggl( (B + A_t X_{t})\,{\textrm{d}} t +\Sigma \,{\textrm{d}} W_{t} + \int_{\mathbb{R}^n\setminus \{0\}} L(X_t,z) \tilde N({\textrm{d}} t, {\textrm{d}} z) \biggr), \\[5pt] {\textrm{d}} A_{t}& = \int_{[0,1]} \int_{[0,1]} \sum_{(j,k)\in S} \textbf{1}_{u \in I_{j,k}( X_{t-}) } Z(j,k, A_{t-}, z) N^\prime ({\textrm{d}} u, {\textrm{d}} t, {\textrm{d}} z). \end{align*}
\begin{align*} {\textrm{d}} X_{t}& =\textrm{diag} (X_{t}) \biggl( (B + A_t X_{t})\,{\textrm{d}} t +\Sigma \,{\textrm{d}} W_{t} + \int_{\mathbb{R}^n\setminus \{0\}} L(X_t,z) \tilde N({\textrm{d}} t, {\textrm{d}} z) \biggr), \\[5pt] {\textrm{d}} A_{t}& = \int_{[0,1]} \int_{[0,1]} \sum_{(j,k)\in S} \textbf{1}_{u \in I_{j,k}( X_{t-}) } Z(j,k, A_{t-}, z) N^\prime ({\textrm{d}} u, {\textrm{d}} t, {\textrm{d}} z). \end{align*}
Here S is the set of ordered pairs of prey species,
![]() $I_{j,k}(x)$
are pairwise disjoint sub-intervals of (0, 1) whose endpoints depend continuously on x, and N
′ is an independent Poisson random measure with intensity measure
$I_{j,k}(x)$
are pairwise disjoint sub-intervals of (0, 1) whose endpoints depend continuously on x, and N
′ is an independent Poisson random measure with intensity measure
![]() $\textrm{Leb} \otimes \textrm{Leb} \otimes \mathfrak{m} $
, with
$\textrm{Leb} \otimes \textrm{Leb} \otimes \mathfrak{m} $
, with
![]() $\mathfrak{m}$
a probability measure on [0, 1]. The length of the interval
$\mathfrak{m}$
a probability measure on [0, 1]. The length of the interval
![]() $I_{j,k}$
, which depends on the state of the community, coincides with the rate at which a change in the foraging strategy involving species j and k is modified: the longer
$I_{j,k}$
, which depends on the state of the community, coincides with the rate at which a change in the foraging strategy involving species j and k is modified: the longer
![]() $I_{j,k}$
is, the more frequently we introduce a change in the coefficients of the interaction matrix through the application of the operator Z. This operator encodes the prey-switching behavior described above. More specifically, if
$I_{j,k}$
is, the more frequently we introduce a change in the coefficients of the interaction matrix through the application of the operator Z. This operator encodes the prey-switching behavior described above. More specifically, if
![]() $\eta=(u, T, z)$
is a point mass of the Poisson random measure N
′ with
$\eta=(u, T, z)$
is a point mass of the Poisson random measure N
′ with
![]() $u \in I_{j,k}(X_{T-})$
, then the interaction matrix is modified as
$u \in I_{j,k}(X_{T-})$
, then the interaction matrix is modified as
 \begin{align*} A^{(1,j)}_{T}& = A^{(1,j)}_{T-} - zA^{(1,j)}_{T-},\\[5pt] A^{(j,1)}_{T}&= A^{(j,1)}_{T-} - zA^{(j,1)}_{T-},\\[5pt] A^{(1,k)}_{T}& = A^{(1,k)}_{T-} + zA^{(1,j)}_{T-},\\[5pt] A^{(k,1)}_{T}&= A^{(k,1)}_{T-} + zA^{(j,1)}_{T-},\end{align*}
\begin{align*} A^{(1,j)}_{T}& = A^{(1,j)}_{T-} - zA^{(1,j)}_{T-},\\[5pt] A^{(j,1)}_{T}&= A^{(j,1)}_{T-} - zA^{(j,1)}_{T-},\\[5pt] A^{(1,k)}_{T}& = A^{(1,k)}_{T-} + zA^{(1,j)}_{T-},\\[5pt] A^{(k,1)}_{T}&= A^{(k,1)}_{T-} + zA^{(j,1)}_{T-},\end{align*}
with all the other entries unchanged. Observe that this modification preserves the sign structure of A, and moreover it preserves the total interaction strengths
![]() $\sum_{j}A^{(1,j)}_t$
and
$\sum_{j}A^{(1,j)}_t$
and
![]() $\sum_{j}A^{(j,1)}_t$
. Thus, if
$\sum_{j}A^{(j,1)}_t$
. Thus, if
![]() $\mathfrak{m}$
is the Lebesgue measure on the unit interval, after normalization the action of Z on both the vector
$\mathfrak{m}$
is the Lebesgue measure on the unit interval, after normalization the action of Z on both the vector
![]() $\bigl(A^{(1,j)}\colon j=2, \ldots, m\bigr)$
and
$\bigl(A^{(1,j)}\colon j=2, \ldots, m\bigr)$
and
![]() $\bigl(-A^{(j,1)}\colon j=2, \ldots, m\bigr)$
is precisely the transition prescribed for the transport process in (1). Moreover, it can be argued on a biological basis that the allowed changes in the foraging efforts are not arbitrary: when the preferred prey has reached low densities, the predator would generally tend to switch to a subset of the potential prey species, and this diet preference imposes certain constraints on the underlying structure of allowed transport of foraging efforts between preys. In the simplest case, i.e. if the predator is a generalist, the transport of foraging efforts from one prey to another can be modeled, in a first approach, through a transport scheme
$\bigl(-A^{(j,1)}\colon j=2, \ldots, m\bigr)$
is precisely the transition prescribed for the transport process in (1). Moreover, it can be argued on a biological basis that the allowed changes in the foraging efforts are not arbitrary: when the preferred prey has reached low densities, the predator would generally tend to switch to a subset of the potential prey species, and this diet preference imposes certain constraints on the underlying structure of allowed transport of foraging efforts between preys. In the simplest case, i.e. if the predator is a generalist, the transport of foraging efforts from one prey to another can be modeled, in a first approach, through a transport scheme
![]() $(G, \textbf{p})$
, with G a directed complete graph and
$(G, \textbf{p})$
, with G a directed complete graph and
![]() $\textbf{p}$
a set of weights assigning equal probability to every possible pair of distinct species. In any case, once this underlying structure is fixed, the transport rules in the last display coincide with the transport process on the corresponding transport scheme.
$\textbf{p}$
a set of weights assigning equal probability to every possible pair of distinct species. In any case, once this underlying structure is fixed, the transport rules in the last display coincide with the transport process on the corresponding transport scheme.
It is well known that in a model such as (2), for any initial condition on the positive orthant, no extinction occurs in finite time a.s., and thus the fundamental question about coexistence translates mathematically into a question about stochastic persistence, namely that no extinction occurs asymptotically. The strongest version of this notion is called strong stochastic persistence, which can be defined as the fact that the system (2) possesses a unique invariant probability measure that does not charge the extinction set
![]() $\bigcup_{i} \{{\bf x}\colon x_i=0 \text{ for at least one } i\}$
. In recent years, much of the literature has successfully tackled the problem of finding operational conditions to ensure strong stochastic persistence of ecological models, at least in the case of dynamics driven by Brownian motion; see e.g. the fundamental paper [Reference Hening and Nguyen6] and the aforementioned paper [Reference Videla18], which deals with the problem of finding conditions for strong stochastic persistence in a Lévy-driven framework. On the other hand, PSB can be considered as a special case of a Holling type III functional response (see [Reference Holling8]) in which predation is low at low densities but saturates quickly at a high value when prey is abundant (see e.g. [Reference Murdoch10]). As has been frequently recognized, prey-switching tends to relax or even remove predation pressure on highly impacted taxa, and thus allows them to recover from low densities (see e.g. [Reference Dunne, Maschner, Betts, Huntly, Russell, Williams and Wood3]) as well as decrease prey competition due to a shared predator. Consequently, the ecological stability of natural ecosystems is enhanced [Reference Teramoto, Kawasaki and Shigesada16, Reference Van Baalen, Křivan, van Rijn and Sabelis17]. It is thus expected that PSB should promote persistence in any suitable model of prey–predator interaction (see [Reference Van Baalen, Křivan, van Rijn and Sabelis17]). This is the phenomenon we aim to quantify via a stochastic version of prey-switching as described above. Specifically, if PSB enhances stability, we wish to understand how much it facilitates the coexistence of species, in comparison with a situation where prey-switching is absent. As a fundamental step toward this end, we need to characterize, as much as possible, the convergence of the pair (X, A) for suitable initial conditions. In this program, a first step is to investigate the dynamics of the matrix component in the simpler, admittedly unrealistic case where the changes of the matrix are independent of the abundances. This means
$\bigcup_{i} \{{\bf x}\colon x_i=0 \text{ for at least one } i\}$
. In recent years, much of the literature has successfully tackled the problem of finding operational conditions to ensure strong stochastic persistence of ecological models, at least in the case of dynamics driven by Brownian motion; see e.g. the fundamental paper [Reference Hening and Nguyen6] and the aforementioned paper [Reference Videla18], which deals with the problem of finding conditions for strong stochastic persistence in a Lévy-driven framework. On the other hand, PSB can be considered as a special case of a Holling type III functional response (see [Reference Holling8]) in which predation is low at low densities but saturates quickly at a high value when prey is abundant (see e.g. [Reference Murdoch10]). As has been frequently recognized, prey-switching tends to relax or even remove predation pressure on highly impacted taxa, and thus allows them to recover from low densities (see e.g. [Reference Dunne, Maschner, Betts, Huntly, Russell, Williams and Wood3]) as well as decrease prey competition due to a shared predator. Consequently, the ecological stability of natural ecosystems is enhanced [Reference Teramoto, Kawasaki and Shigesada16, Reference Van Baalen, Křivan, van Rijn and Sabelis17]. It is thus expected that PSB should promote persistence in any suitable model of prey–predator interaction (see [Reference Van Baalen, Křivan, van Rijn and Sabelis17]). This is the phenomenon we aim to quantify via a stochastic version of prey-switching as described above. Specifically, if PSB enhances stability, we wish to understand how much it facilitates the coexistence of species, in comparison with a situation where prey-switching is absent. As a fundamental step toward this end, we need to characterize, as much as possible, the convergence of the pair (X, A) for suitable initial conditions. In this program, a first step is to investigate the dynamics of the matrix component in the simpler, admittedly unrealistic case where the changes of the matrix are independent of the abundances. This means
![]() $I_{j,k}$
constant intervals. As the reader can easily convince herself, this amounts to studying ergodic properties of the transport process as a Markov chain in its own right.
$I_{j,k}$
constant intervals. As the reader can easily convince herself, this amounts to studying ergodic properties of the transport process as a Markov chain in its own right.
This is the aim of the forthcoming sections.
2. Basic analytic properties
In this short section we provide some simple results that guarantee the existence of invariant measures.
For arbitrary functions
![]() $f\colon V \mapsto \mathbb{R}$
, consider the Laplace functionals
$f\colon V \mapsto \mathbb{R}$
, consider the Laplace functionals
![]() $\Delta_V \ni \mu \mapsto {\textrm{e}}^{\langle \mu, f \rangle } \in \mathbb{R}_+$
. For
$\Delta_V \ni \mu \mapsto {\textrm{e}}^{\langle \mu, f \rangle } \in \mathbb{R}_+$
. For
![]() $\mu \in \Delta_{V}$
we easily compute
$\mu \in \Delta_{V}$
we easily compute
 \begin{align} \mathbb{E}_{\mu} \bigl({\textrm{e}}^{\langle \mu_{1}, f\rangle }\bigr) = {\textrm{e}}^{\langle \mu, f\rangle} \Biggl( \sum_{ij \in E} p_{ij} \dfrac{{\textrm{e}}^{ \mu^{(i)} (f(j) - f(i)) }-1}{\mu^{(i)} (f(j)-f(i)) } \Biggr).\end{align}
\begin{align} \mathbb{E}_{\mu} \bigl({\textrm{e}}^{\langle \mu_{1}, f\rangle }\bigr) = {\textrm{e}}^{\langle \mu, f\rangle} \Biggl( \sum_{ij \in E} p_{ij} \dfrac{{\textrm{e}}^{ \mu^{(i)} (f(j) - f(i)) }-1}{\mu^{(i)} (f(j)-f(i)) } \Biggr).\end{align}
Observe that if
![]() $(\mu(k))_{k \ge 0}$
is a sequence such that
$(\mu(k))_{k \ge 0}$
is a sequence such that
![]() $\langle \mu(k), f \rangle \rightarrow \langle \hat \mu, f\rangle$
for some probability measure
$\langle \mu(k), f \rangle \rightarrow \langle \hat \mu, f\rangle$
for some probability measure
![]() $\hat \mu$
and for every f (which is simply weak convergence of probability measures when
$\hat \mu$
and for every f (which is simply weak convergence of probability measures when
![]() $\Delta_V$
is identified with
$\Delta_V$
is identified with
![]() $\mathcal{P}(V)$
), then
$\mathcal{P}(V)$
), then
![]() $ \mathbb{E}_{\mu(k)} \bigl( {\textrm{e}}^{ \langle \mu_1, f \rangle} \bigr)$
converges to
$ \mathbb{E}_{\mu(k)} \bigl( {\textrm{e}}^{ \langle \mu_1, f \rangle} \bigr)$
converges to
![]() $\mathbb{E}_{\hat \mu} \bigl( {\textrm{e}}^{ \langle \mu_1, f \rangle} \bigr) $
for every f as well. On the other hand, since V is finite, the convergence
$\mathbb{E}_{\hat \mu} \bigl( {\textrm{e}}^{ \langle \mu_1, f \rangle} \bigr) $
for every f as well. On the other hand, since V is finite, the convergence
![]() $\langle \mu(k), f \rangle \rightarrow \langle \hat \mu, f\rangle$
for some probability measure
$\langle \mu(k), f \rangle \rightarrow \langle \hat \mu, f\rangle$
for some probability measure
![]() $\hat \mu$
and for every f is equivalent to pointwise convergence of
$\hat \mu$
and for every f is equivalent to pointwise convergence of
![]() $\mu (k) $
to
$\mu (k) $
to
![]() $\hat \mu$
when the elements of
$\hat \mu$
when the elements of
![]() $\Delta_V$
are considered as vectors indexed by V.
$\Delta_V$
are considered as vectors indexed by V.
Proposition 1. The process
![]() $(\mu_n\colon n \ge 0)$
is a Feller chain.
$(\mu_n\colon n \ge 0)$
is a Feller chain.
Proof. By the discussion above,
![]() $PG(\mu(k)) \to PG (\mu)$
whenever G is a Laplace functional and
$PG(\mu(k)) \to PG (\mu)$
whenever G is a Laplace functional and
![]() $\mu(k) \to \mu$
weakly. Now let
$\mu(k) \to \mu$
weakly. Now let
![]() $F \in \mathcal{C} (\Delta_V)$
be an arbitrary continuous function on
$F \in \mathcal{C} (\Delta_V)$
be an arbitrary continuous function on
![]() $\Delta_V$
, fix
$\Delta_V$
, fix
![]() $\varepsilon > 0$
, and again consider a sequence
$\varepsilon > 0$
, and again consider a sequence
![]() $\mu(k)$
converging to
$\mu(k)$
converging to
![]() $\mu$
weakly. Let G be a finite linear combination of functions of the form
$\mu$
weakly. Let G be a finite linear combination of functions of the form
![]() $\mu \mapsto {\textrm{e}}^{\langle \mu, f \rangle}$
that uniformly approximates the function F up to
$\mu \mapsto {\textrm{e}}^{\langle \mu, f \rangle}$
that uniformly approximates the function F up to
![]() $\varepsilon/3$
. Such a function exists by the Stone–Weierstrass theorem. Fix
$\varepsilon/3$
. Such a function exists by the Stone–Weierstrass theorem. Fix
![]() $k_0 > 0$
such that
$k_0 > 0$
such that
![]() $\vert PG (\mu (k))- PG (\mu)\vert $
for every
$\vert PG (\mu (k))- PG (\mu)\vert $
for every
![]() $k \ge k_0$
. Plainly
$k \ge k_0$
. Plainly
 \begin{align*} & \vert PF (\mu (k))- PF (\mu)\vert \\[5pt] & \quad \le \vert PF (\mu (k))- PG (\mu(k))\vert + \vert PG (\mu (k))- PG (\mu)\vert + \vert PG (\mu )- PF (\mu)\vert \\[5pt] & \quad \le \mathbb{E}_{\mu (k)} ( \vert F (\mu_1)- G (\mu_1) \vert ) + \vert PG (\mu (k))- PG (\mu)\vert + \mathbb{E}_{\mu} ( \vert G (\mu_1)- F (\mu_1) \vert ) \\[5pt] & \quad\le \dfrac{\varepsilon}{3} + \vert PG (\mu (k))- PG (\mu)\vert + \dfrac{\varepsilon}{3},\end{align*}
\begin{align*} & \vert PF (\mu (k))- PF (\mu)\vert \\[5pt] & \quad \le \vert PF (\mu (k))- PG (\mu(k))\vert + \vert PG (\mu (k))- PG (\mu)\vert + \vert PG (\mu )- PF (\mu)\vert \\[5pt] & \quad \le \mathbb{E}_{\mu (k)} ( \vert F (\mu_1)- G (\mu_1) \vert ) + \vert PG (\mu (k))- PG (\mu)\vert + \mathbb{E}_{\mu} ( \vert G (\mu_1)- F (\mu_1) \vert ) \\[5pt] & \quad\le \dfrac{\varepsilon}{3} + \vert PG (\mu (k))- PG (\mu)\vert + \dfrac{\varepsilon}{3},\end{align*}
and we deduce that the last expression is no greater than
![]() $\varepsilon$
whenever
$\varepsilon$
whenever
![]() $k \ge k_0$
. The result follows.
$k \ge k_0$
. The result follows.![]()
Corollary 1. P admits invariant measures.
Proof.
![]() $\Delta_V$
is compact and, by Proposition 1, the chain is Feller. The result follows from the well-known Bogolyubov–Krylov theorem.
$\Delta_V$
is compact and, by Proposition 1, the chain is Feller. The result follows from the well-known Bogolyubov–Krylov theorem.![]()
3. The simplest case
In this section we specialize the previous discussion to the case
![]() $\vert V\vert =m=2$
, and for simplicity we first consider
$\vert V\vert =m=2$
, and for simplicity we first consider
![]() $p_{ij}=p_{ji}=\frac{1}{2}$
for
$p_{ij}=p_{ji}=\frac{1}{2}$
for
![]() $i \neq j$
. Observe that in this case every probability measure on
$i \neq j$
. Observe that in this case every probability measure on
![]() $\Delta_V$
is completely described by a random variable X supported on [0, 1] via the prescription
$\Delta_V$
is completely described by a random variable X supported on [0, 1] via the prescription
![]() $\mu^{(1)}=X, \mu^{(2)}=1-X$
. Indeed, it is easily seen that the description of the process
$\mu^{(1)}=X, \mu^{(2)}=1-X$
. Indeed, it is easily seen that the description of the process
![]() $\bigl(\mu^{(1)}_n\colon n \ge 0\bigr)$
is equivalent to the next one. Let
$\bigl(\mu^{(1)}_n\colon n \ge 0\bigr)$
is equivalent to the next one. Let
![]() $(U_n\colon n\ge 1 )$
be a family of independent and identically distributed (i.i.d.)
$(U_n\colon n\ge 1 )$
be a family of independent and identically distributed (i.i.d.)
![]() $\operatorname{Uniform}([0,1])$
random variables, and let
$\operatorname{Uniform}([0,1])$
random variables, and let
![]() $(Y_{n}\colon n \ge 1)$
be an i.i.d. sequence of
$(Y_{n}\colon n \ge 1)$
be an i.i.d. sequence of
![]() $\operatorname{Bernoulli}(1/2)$
random variables, both defined on the same probability space
$\operatorname{Bernoulli}(1/2)$
random variables, both defined on the same probability space
![]() $(\Omega, \mathbb{P})$
. Given an initial condition
$(\Omega, \mathbb{P})$
. Given an initial condition
![]() $X_0$
, consider the discrete-parameter random dynamical systems
$X_0$
, consider the discrete-parameter random dynamical systems
 \begin{equation*} X_{n+1}= \begin{cases} X_n -X_n U_{n+1} & \text{if $ Y_{n+1}=0$,}\\[5pt] X_n + (1-X_n)U_{n+1} & \text{if $ Y_{n+1}=1$.} \end{cases} \end{equation*}
\begin{equation*} X_{n+1}= \begin{cases} X_n -X_n U_{n+1} & \text{if $ Y_{n+1}=0$,}\\[5pt] X_n + (1-X_n)U_{n+1} & \text{if $ Y_{n+1}=1$.} \end{cases} \end{equation*}
Then
![]() $(X_n\colon n \ge 0)$
has the same law as
$(X_n\colon n \ge 0)$
has the same law as
![]() $\bigl(\mu_{n}^{(1)}\bigr)$
for the same initial condition.
$\bigl(\mu_{n}^{(1)}\bigr)$
for the same initial condition.
Proposition 2. The unique invariant probability measure of the process
![]() $(X_n\colon n\ge 0)$
is given by the
$(X_n\colon n\ge 0)$
is given by the
![]() $\operatorname{arcsine}$
distribution, i.e. the absolutely continuous probability measure on (0, 1) with density
$\operatorname{arcsine}$
distribution, i.e. the absolutely continuous probability measure on (0, 1) with density
Proof. To ease notation, write
![]() $X=X_0$
,
$X=X_0$
,
![]() $U_1=U$
. For
$U_1=U$
. For
![]() $t \in (0,1)$
, we compute
$t \in (0,1)$
, we compute
 \begin{align} \mathbb{P} (X_1 \le t) & = \dfrac{1}{2} ( \mathbb{P} (X_1 \le t \mid Y_1 = 0) + \mathbb{P} (X_1\le t \mid Y_1=1) ) \nonumber \\[5pt] & = \dfrac{1}{2} ( \mathbb{P} (X (1-U) \le t) + \mathbb{P} (X+U(1-X) \le t ) ) \nonumber \\[5pt] &= \dfrac{1}{2} \biggl( \mathbb{P} \biggl(U \ge \dfrac{X-t}{X}\biggr) + \mathbb{P} \biggl(U \le \dfrac{t-X}{1-X} \biggr) \biggr) \nonumber \\[5pt] & = \dfrac{1}{2} \biggl( \mathbb{P} \biggl(U \ge \dfrac{X-t}{X}, X > t\biggr) + \mathbb{P} (X \le t) + \mathbb{P} \biggl(U \le \dfrac{t-X}{1-X}, X \le t \biggr) \biggr).\end{align}
\begin{align} \mathbb{P} (X_1 \le t) & = \dfrac{1}{2} ( \mathbb{P} (X_1 \le t \mid Y_1 = 0) + \mathbb{P} (X_1\le t \mid Y_1=1) ) \nonumber \\[5pt] & = \dfrac{1}{2} ( \mathbb{P} (X (1-U) \le t) + \mathbb{P} (X+U(1-X) \le t ) ) \nonumber \\[5pt] &= \dfrac{1}{2} \biggl( \mathbb{P} \biggl(U \ge \dfrac{X-t}{X}\biggr) + \mathbb{P} \biggl(U \le \dfrac{t-X}{1-X} \biggr) \biggr) \nonumber \\[5pt] & = \dfrac{1}{2} \biggl( \mathbb{P} \biggl(U \ge \dfrac{X-t}{X}, X > t\biggr) + \mathbb{P} (X \le t) + \mathbb{P} \biggl(U \le \dfrac{t-X}{1-X}, X \le t \biggr) \biggr).\end{align}
Assume now that X has a density with respect to Lebesgue measure on the unit interval. Let g be such a density, and so
![]() $G'= g$
Lebesgue a.s. on (0, 1). Then, by independence between X and U,
$G'= g$
Lebesgue a.s. on (0, 1). Then, by independence between X and U,
 \begin{align*} \mathbb{P} (X_1 \le t) & = \dfrac{1}{2} \biggl( \mathbb{P} (X \le t) + \mathbb{P} \biggl(U \ge \dfrac{X-t}{X}, X > t\biggr) + \mathbb{P} \biggl(U \le \dfrac{t-X}{1-X}, X \le t \biggr) \biggr) \\[5pt] &= \dfrac{1}{2} \biggl( G(t) + \int_{t}^1 \biggl( 1- \dfrac{x-t}{x}\biggr)g(x)\,{\textrm{d}} x + \int_{0}^t \biggl( \dfrac{t-1}{1-x} + 1 \biggr) g(x)\,{\textrm{d}} x\biggr)\\[5pt] &= \dfrac{1}{2} \biggl( G(t) + t \int_{t}^1 \dfrac{1}{x}g(x)\,{\textrm{d}} x - (1-t)\int_{0}^t \dfrac{1}{1-x} g(x)\,{\textrm{d}} x + G(t) \biggr)\\[5pt] &= G(t) + \dfrac{1}{2} \biggl( t \int_{t}^1 \dfrac{1}{x}g(x)\,{\textrm{d}} x - (1-t)\int_{0}^t \dfrac{1}{1-x} g(x)\,{\textrm{d}} x \biggr).\end{align*}
\begin{align*} \mathbb{P} (X_1 \le t) & = \dfrac{1}{2} \biggl( \mathbb{P} (X \le t) + \mathbb{P} \biggl(U \ge \dfrac{X-t}{X}, X > t\biggr) + \mathbb{P} \biggl(U \le \dfrac{t-X}{1-X}, X \le t \biggr) \biggr) \\[5pt] &= \dfrac{1}{2} \biggl( G(t) + \int_{t}^1 \biggl( 1- \dfrac{x-t}{x}\biggr)g(x)\,{\textrm{d}} x + \int_{0}^t \biggl( \dfrac{t-1}{1-x} + 1 \biggr) g(x)\,{\textrm{d}} x\biggr)\\[5pt] &= \dfrac{1}{2} \biggl( G(t) + t \int_{t}^1 \dfrac{1}{x}g(x)\,{\textrm{d}} x - (1-t)\int_{0}^t \dfrac{1}{1-x} g(x)\,{\textrm{d}} x + G(t) \biggr)\\[5pt] &= G(t) + \dfrac{1}{2} \biggl( t \int_{t}^1 \dfrac{1}{x}g(x)\,{\textrm{d}} x - (1-t)\int_{0}^t \dfrac{1}{1-x} g(x)\,{\textrm{d}} x \biggr).\end{align*}
Let
![]() $\hat h(t)$
be the derivative of the left-hand side. Differentiation yields
$\hat h(t)$
be the derivative of the left-hand side. Differentiation yields
Thus, if
![]() $(X_{n}\colon n\ge 0)$
possesses a continuous invariant density, by the above equation it is differentiable and must thus satisfy
$(X_{n}\colon n\ge 0)$
possesses a continuous invariant density, by the above equation it is differentiable and must thus satisfy
whose unique solution integrating up to 1 is given by the arcsine law. Thus h is the unique continuous invariant density for the dynamical system
![]() $(X_n\colon n\ge 0)$
.
$(X_n\colon n\ge 0)$
.
Now let P
′ be the transition kernel of the chain
![]() $X_n$
. For a Borel set A and
$X_n$
. For a Borel set A and
![]() $x \in (0,1)$
, we easily compute
$x \in (0,1)$
, we easily compute
For small
![]() $h > 0$
, we obtain the straightforward estimate
$h > 0$
, we obtain the straightforward estimate
Thus the first term in (6) is the expression of a continuous function on (0, 1). A similar estimate for the second term above shows that
![]() $P'\textbf{1}_A$
is continuous on (0, 1). By a standard approximation argument, P
′ f is continuous for every bounded Borel function f. Thus P
′ possesses the strong Feller property. On the other hand, the above computation also shows that every point in [0, 1] is accessible for the chain, in the sense that for every
$P'\textbf{1}_A$
is continuous on (0, 1). By a standard approximation argument, P
′ f is continuous for every bounded Borel function f. Thus P
′ possesses the strong Feller property. On the other hand, the above computation also shows that every point in [0, 1] is accessible for the chain, in the sense that for every
![]() $U_x$
open neighborhood of x, and for every
$U_x$
open neighborhood of x, and for every
![]() $z \in [0,1]$
, there exists a
$z \in [0,1]$
, there exists a
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $P^k (z, U_x)> 0$
. It is well known that every strong Feller Markov chain with at least one accessible point has at most one invariant measure (see e.g. [Reference Hairer5, Proposition 2.7]). We deduce that the arcsine law is the unique invariant probability measure of the process.
$P^k (z, U_x)> 0$
. It is well known that every strong Feller Markov chain with at least one accessible point has at most one invariant measure (see e.g. [Reference Hairer5, Proposition 2.7]). We deduce that the arcsine law is the unique invariant probability measure of the process.![]()
The above proof is easily extended to the non-symmetric case. Indeed, if we put
![]() $p=p_{12}$
,
$p=p_{12}$
,
![]() $q=p_{21}$
, equation (4) above becomes
$q=p_{21}$
, equation (4) above becomes
and proceeding through the same steps detailed in the proof, equation (5) becomes
From this point on, the argument works in exactly the same way, and we arrive at the following result.
Proposition 3. The unique invariant measure of the process
![]() $(\mu_{k}\colon k \ge 0)$
in the case
$(\mu_{k}\colon k \ge 0)$
in the case
![]() $m=2$
is the Beta distribution with density
$m=2$
is the Beta distribution with density
![]() $\operatorname{Beta}\!(p_{ji},p_{ij})$
, i.e. the probability measure on [0, 1] with density
$\operatorname{Beta}\!(p_{ji},p_{ij})$
, i.e. the probability measure on [0, 1] with density
Still in the case
![]() $m=2$
, let
$m=2$
, let
![]() $\pi$
be the invariant measure identified above. We now state the geometric convergence of the transition operator to the measure
$\pi$
be the invariant measure identified above. We now state the geometric convergence of the transition operator to the measure
![]() $\pi$
.
$\pi$
.
Theorem 4. There exist constants
![]() $C > 0$
,
$C > 0$
,
![]() $\eta \in (0,1)$
such that
$\eta \in (0,1)$
such that
for every bounded measurable function
![]() $f\colon [0,1] \mapsto \mathbb{R}$
.
$f\colon [0,1] \mapsto \mathbb{R}$
.
Proof. Let
![]() $x, y \in [0,1]$
, and assume
$x, y \in [0,1]$
, and assume
![]() $x<y$
. Then
$x<y$
. Then
 \begin{align*} & P' (x, {\textrm{d}} z)- P'(y, {\textrm{d}} z)\\[5pt] & \quad = {\textrm{d}} z \biggl( p \textbf{1}_{z < x }\dfrac{1}{x} + q \textbf{1}_{z> x}\dfrac{1}{1-x} - p \textbf{1}_{z < y }\dfrac{1}{y} - q \textbf{1}_{z> y}\dfrac{1}{1-y}\biggr)\\[5pt] &\quad ={\textrm{d}} z \biggl( p \textbf{1}_{z<x} \biggl[\dfrac{1}{x}-\dfrac{1}{y} \biggr] + q \textbf{1}_{z>y}\biggl[ \dfrac{1}{1-x}-\dfrac{1}{1-y} \biggr] + \textbf{1}{z\in (x,y)} \biggl[ \dfrac{q}{1-x}- \dfrac{p}{y}\biggr] \biggr) .\end{align*}
\begin{align*} & P' (x, {\textrm{d}} z)- P'(y, {\textrm{d}} z)\\[5pt] & \quad = {\textrm{d}} z \biggl( p \textbf{1}_{z < x }\dfrac{1}{x} + q \textbf{1}_{z> x}\dfrac{1}{1-x} - p \textbf{1}_{z < y }\dfrac{1}{y} - q \textbf{1}_{z> y}\dfrac{1}{1-y}\biggr)\\[5pt] &\quad ={\textrm{d}} z \biggl( p \textbf{1}_{z<x} \biggl[\dfrac{1}{x}-\dfrac{1}{y} \biggr] + q \textbf{1}_{z>y}\biggl[ \dfrac{1}{1-x}-\dfrac{1}{1-y} \biggr] + \textbf{1}{z\in (x,y)} \biggl[ \dfrac{q}{1-x}- \dfrac{p}{y}\biggr] \biggr) .\end{align*}
Let
![]() $\varphi\colon [0,1] \mapsto \mathbb{R}$
be a measurable function with
$\varphi\colon [0,1] \mapsto \mathbb{R}$
be a measurable function with
![]() $ \vert \varphi (x)\vert \le 1$
-Lebesgue a.e. By virtue of the above computation,
$ \vert \varphi (x)\vert \le 1$
-Lebesgue a.e. By virtue of the above computation,
 \begin{align*} & \vert P'\varphi (x)- P' \varphi (y)\vert \\[5pt] &\quad \le \dfrac{p(y-x)}{xy} \int_{0}^x \vert \varphi (z)\vert \,{\textrm{d}} z + \dfrac{q(y-x)}{(1-x)(1-y)} \int_{y}^1 \vert \varphi (z)\vert \,{\textrm{d}} z + \dfrac{\vert p-px-qy\vert}{(1-x)y} \int_{x}^y \vert \varphi (z)\vert \,{\textrm{d}} z \\[5pt] & \quad = (y-x )\biggl( \dfrac{p}{y} + \dfrac{q}{1-x} + \dfrac{\max\!(p-px-qy, qy +px-p}{(1-x)y} \biggr) \\[5pt] &\quad= (y-x) \max \biggl( \dfrac{2p}{y}, \dfrac{2q}{1-x} \biggr)\\[5pt] &\quad= \max \biggl( 2p \biggl[ 1- \dfrac{x}{y} \biggr], 2q \biggl[ 1- \dfrac{1-y}{1-x} \biggr]\biggr) \\[5pt] &\quad \le 1.\end{align*}
\begin{align*} & \vert P'\varphi (x)- P' \varphi (y)\vert \\[5pt] &\quad \le \dfrac{p(y-x)}{xy} \int_{0}^x \vert \varphi (z)\vert \,{\textrm{d}} z + \dfrac{q(y-x)}{(1-x)(1-y)} \int_{y}^1 \vert \varphi (z)\vert \,{\textrm{d}} z + \dfrac{\vert p-px-qy\vert}{(1-x)y} \int_{x}^y \vert \varphi (z)\vert \,{\textrm{d}} z \\[5pt] & \quad = (y-x )\biggl( \dfrac{p}{y} + \dfrac{q}{1-x} + \dfrac{\max\!(p-px-qy, qy +px-p}{(1-x)y} \biggr) \\[5pt] &\quad= (y-x) \max \biggl( \dfrac{2p}{y}, \dfrac{2q}{1-x} \biggr)\\[5pt] &\quad= \max \biggl( 2p \biggl[ 1- \dfrac{x}{y} \biggr], 2q \biggl[ 1- \dfrac{1-y}{1-x} \biggr]\biggr) \\[5pt] &\quad \le 1.\end{align*}
This is a sufficient condition to apply Harris’s theorem in the compact state-space case (see [Reference Hairer5]), and this concludes the proof.![]()
4. The general case
Let us come back to the general model:
![]() $G=(V, E)$
is a directed, strongly connected graph, and
$G=(V, E)$
is a directed, strongly connected graph, and
![]() $\textbf{p}$
is a probability vector indexed by the edges with
$\textbf{p}$
is a probability vector indexed by the edges with
![]() $p_{ij}> 0$
if and only if
$p_{ij}> 0$
if and only if
![]() $ij \in E$
. Recall that P is the transition kernel of the chain. Observe that whenever
$ij \in E$
. Recall that P is the transition kernel of the chain. Observe that whenever
![]() $m > 2$
, P is, in general, a degenerate transition operator, in the sense that it does not possess a density. Thus, to prove uniqueness of the invariant law, we cannot rely directly on P, and in fact we will need to prove some properties for higher-order iterates of P.
$m > 2$
, P is, in general, a degenerate transition operator, in the sense that it does not possess a density. Thus, to prove uniqueness of the invariant law, we cannot rely directly on P, and in fact we will need to prove some properties for higher-order iterates of P.
For this part we will need the following condition to hold.
Assumption 1.
![]() $uv \in E \Leftrightarrow vu \in E$
.
$uv \in E \Leftrightarrow vu \in E$
.
The connectedness of G is the least we can ask from the underlying structure in order to guarantee uniqueness of the invariant measure. As for the above condition, we will need it in order to guarantee that any spanning tree of (the undirected version of) G can be regarded as a strongly connected subgraph of (the directed version of) G.
4.1. A transport algorithm with density
We introduce some extra notation. For any finite set V and
![]() $z > 0$
, we write
$z > 0$
, we write
![]() $z \Delta_V $
to denote the set of positive vectors indexed by V with
$z \Delta_V $
to denote the set of positive vectors indexed by V with
![]() $\sum_{v \in V} x_v= z$
. The notation is consistent, since
$\sum_{v \in V} x_v= z$
. The notation is consistent, since
![]() $\Delta_V= 1 \Delta_V$
. Let
$\Delta_V= 1 \Delta_V$
. Let
![]() $G=(V, E)$
be a finite directed graph. For two points
$G=(V, E)$
be a finite directed graph. For two points
![]() $x, y \in z \Delta_V$
, we say that there exists a move that takes x into y if there exists an edge
$x, y \in z \Delta_V$
, we say that there exists a move that takes x into y if there exists an edge
![]() $uv \in E$
such that
$uv \in E$
such that
![]() $y_w=x_w$
for every
$y_w=x_w$
for every
![]() $w \neq u, v$
and
$w \neq u, v$
and
![]() $x_u \ge y_u$
. In this case we write
$x_u \ge y_u$
. In this case we write
![]() $x \rightarrow y$
. The move is non-trivial if
$x \rightarrow y$
. The move is non-trivial if
![]() $x_u >y_u$
, and in this case we write
$x_u >y_u$
, and in this case we write
Fix
![]() $x \in z \Delta_V$
. We say that
$x \in z \Delta_V$
. We say that
![]() $y\in z \Delta_V$
is reachable from x if there exists a finite sequence of moves
$y\in z \Delta_V$
is reachable from x if there exists a finite sequence of moves
![]() $x \rightarrow x_1 \rightarrow x_2 \rightarrow \cdots \rightarrow x_{n-1} \rightarrow y$
. Let
$x \rightarrow x_1 \rightarrow x_2 \rightarrow \cdots \rightarrow x_{n-1} \rightarrow y$
. Let
![]() $\mathcal{R}_x$
be the set of points in
$\mathcal{R}_x$
be the set of points in
![]() $z \Delta_V$
reachable from x in one non-trivial move, and in general, for
$z \Delta_V$
reachable from x in one non-trivial move, and in general, for
![]() $j \ge 1$
, let
$j \ge 1$
, let
![]() $\mathcal{R}_x^j$
be the set of points that are reachable from x in j non-trivial moves, i.e. the points y such that there exist j non-trivial moves that take x into y. Clearly
$\mathcal{R}_x^j$
be the set of points that are reachable from x in j non-trivial moves, i.e. the points y such that there exist j non-trivial moves that take x into y. Clearly
Lemma 1. Let V be a set with
![]() $\vert V \vert =m$
, and let
$\vert V \vert =m$
, and let
![]() $G=(V, E)$
be a finite strongly connected digraph that satisfies Assumption 1. Let
$G=(V, E)$
be a finite strongly connected digraph that satisfies Assumption 1. Let
![]() $z > 0$
, and fix
$z > 0$
, and fix
![]() $x \in z \Delta_V$
. Then
$x \in z \Delta_V$
. Then
In words: almost every point is reachable in exactly
![]() $m-1$
non-trivial moves.
$m-1$
non-trivial moves.
Proof. Observe first that we can reduce the problem to the case where G is a tree, since the general situation follows by considering that the moves are constrained to be made on a fixed spanning tree of G.
So, let G be a tree. We will prove the following claim by induction on the number of vertices of G:
-
(Pm) For every tree
 $G=(V, E)$
on m vertices, for every
$G=(V, E)$
on m vertices, for every
 $z> 0$
, every
$z> 0$
, every
 $x \in z \Delta_V$
and almost every
$x \in z \Delta_V$
and almost every
 $y \in z \Delta_V$
, there exists a sequence of
$y \in z \Delta_V$
, there exists a sequence of
 $m-1$
non-trivial moves that takes x into y.
$m-1$
non-trivial moves that takes x into y.
In order to prove the claim, for G, m, z, x, and y as above, we will define recursively a particular sequence of
![]() $m-1$
non-trivial moves, hereafter denoted
$m-1$
non-trivial moves, hereafter denoted
![]() $t_{G, z} (x, y)$
, that takes x into y.
$t_{G, z} (x, y)$
, that takes x into y.
If G is the tree on the vertices
![]() $\{1, 2\}$
, the claim is obviously true: either
$\{1, 2\}$
, the claim is obviously true: either
![]() $x_1> y_1$
or
$x_1> y_1$
or
![]() $x_2 \ge y_2$
. In the first case let
$x_2 \ge y_2$
. In the first case let
and in the second case define
Observe that equality above arises only in a set of null Lebesgue measure.
Now suppose that
![]() ${\bf (P_k)}$
holds for
${\bf (P_k)}$
holds for
![]() $k=2, 3, \ldots, m-1$
, and let G be a tree on m vertices. We proceed by pruning the tree of its leaves. Let v be a leaf of G and let u be its unique parent in G. We distinguish two cases.
$k=2, 3, \ldots, m-1$
, and let G be a tree on m vertices. We proceed by pruning the tree of its leaves. Let v be a leaf of G and let u be its unique parent in G. We distinguish two cases.
Case I:
![]() $x_v > y_v$
. Define the auxiliary configurations x
′ and y
′ on the
$x_v > y_v$
. Define the auxiliary configurations x
′ and y
′ on the
![]() $m-1$
vertices of the tree
$m-1$
vertices of the tree
![]() $G \setminus \{v\}$
as follows:
$G \setminus \{v\}$
as follows:
![]() $x'_{\!\!i}=x_i$
for
$x'_{\!\!i}=x_i$
for
![]() $i\neq u, v$
,
$i\neq u, v$
,
![]() $x'_{\!\!u}=x_u+x_v-y_v$
,
$x'_{\!\!u}=x_u+x_v-y_v$
,
![]() $y'_{\!\!i}=y_i, i \neq v$
. Define
$y'_{\!\!i}=y_i, i \neq v$
. Define
![]() $t_{G, z}(x, y)$
as the concatenation of
$t_{G, z}(x, y)$
as the concatenation of
followed by
![]() $t_{G \setminus \{v\}, z-y_v}(x', y')$
, or with our notation
$t_{G \setminus \{v\}, z-y_v}(x', y')$
, or with our notation
Case II:
![]() $x_v \le y_v$
. In this case we define the auxiliary configurations x
′′ and y
′′ on the tree
$x_v \le y_v$
. In this case we define the auxiliary configurations x
′′ and y
′′ on the tree
![]() $G \setminus \{v\}$
as follows:
$G \setminus \{v\}$
as follows:
![]() $x''_{\!\!\!i}=x_i$
for
$x''_{\!\!\!i}=x_i$
for
![]() $i\neq v$
,
$i\neq v$
,
![]() $y''_{\!\!\!i}=y_i$
for
$y''_{\!\!\!i}=y_i$
for
![]() $i \neq u, v$
, and
$i \neq u, v$
, and
![]() $y''_{\!\!\!u}=y_u+y_v-x_v$
. The required sequence
$y''_{\!\!\!u}=y_u+y_v-x_v$
. The required sequence
![]() $t_{G, z}(x, y)$
is given by the concatenation of
$t_{G, z}(x, y)$
is given by the concatenation of
![]() $t_{G\setminus\{v\}, z-x_v}(x'', y'')$
followed by the move
$t_{G\setminus\{v\}, z-x_v}(x'', y'')$
followed by the move
or
In any case, by our induction hypothesis, we have proved that when G is a tree, the transport operation from configuration x to y can be performed in exactly
![]() $m-1$
moves. Some of these moves, of course, may well be trivial moves, in that the second case in the description of the algorithm may occur with equality. We now show that for fixed x this can occur on a set of null Lebesgue measure. For every proper subset
$m-1$
moves. Some of these moves, of course, may well be trivial moves, in that the second case in the description of the algorithm may occur with equality. We now show that for fixed x this can occur on a set of null Lebesgue measure. For every proper subset
![]() $J\subset V$
and constants
$J\subset V$
and constants
![]() $\epsilon_i, \eta_i, i \in J$
with
$\epsilon_i, \eta_i, i \in J$
with
![]() $\vert \epsilon_i\vert = \vert \eta_i\vert =1$
, define
$\vert \epsilon_i\vert = \vert \eta_i\vert =1$
, define
![]() $\mathcal{N}_{J, \epsilon, \eta}$
as the set
$\mathcal{N}_{J, \epsilon, \eta}$
as the set
 \begin{align*} \mathcal{N}_{J, \epsilon, \eta} \;:\!=\; \Biggl\{y \in \Delta_V\colon \sum_{i \in J}\epsilon_i y_i= \sum_{j \in J}\eta_j x_j\Biggr\}.\end{align*}
\begin{align*} \mathcal{N}_{J, \epsilon, \eta} \;:\!=\; \Biggl\{y \in \Delta_V\colon \sum_{i \in J}\epsilon_i y_i= \sum_{j \in J}\eta_j x_j\Biggr\}.\end{align*}
Then
![]() $\mathcal{N}_{J, \epsilon, \eta}$
is a proper linear sub-manifold of
$\mathcal{N}_{J, \epsilon, \eta}$
is a proper linear sub-manifold of
![]() $\Delta_V$
, and thus has null Lebesgue measure. The same holds, of course, for the finite union
$\Delta_V$
, and thus has null Lebesgue measure. The same holds, of course, for the finite union
![]() $\mathcal{N}\;:\!=\; \bigcup_{J, \epsilon, \eta} \mathcal{N}_{J, \epsilon, \eta}$
. Now the algorithm we have provided above shows that
$\mathcal{N}\;:\!=\; \bigcup_{J, \epsilon, \eta} \mathcal{N}_{J, \epsilon, \eta}$
. Now the algorithm we have provided above shows that
![]() $t_{G, z}(x, y)$
is made up of less than
$t_{G, z}(x, y)$
is made up of less than
![]() $m-1$
non-trivial moves on a y-set where Case II above, at some point in the recursive application of the algorithm, holds with equality. But this set is obviously contained in
$m-1$
non-trivial moves on a y-set where Case II above, at some point in the recursive application of the algorithm, holds with equality. But this set is obviously contained in
![]() $\mathcal{N}$
.
$\mathcal{N}$
.![]()
The proof of the above theorem indeed shows that
![]() $P^{m-1}$
has a continuous component that has a density with respect to Lebesgue measure. Indeed, by the computation (6), this claim holds true when G has two vertices. Assume it is true for graphs with at most
$P^{m-1}$
has a continuous component that has a density with respect to Lebesgue measure. Indeed, by the computation (6), this claim holds true when G has two vertices. Assume it is true for graphs with at most
![]() $m-1$
vertices for which Assumption 1 holds, and let G be a finite digraph on m vertices satisfying Assumption 1. Let T be a fixed spanning tree of G when considered as an undirected graph. Define the weight of T as
$m-1$
vertices for which Assumption 1 holds, and let G be a finite digraph on m vertices satisfying Assumption 1. Let T be a fixed spanning tree of G when considered as an undirected graph. Define the weight of T as
![]() $w_T\;:\!=\; \prod_{e \in T}p_e$
. Fix
$w_T\;:\!=\; \prod_{e \in T}p_e$
. Fix
![]() $x \in \Delta_V$
. Let
$x \in \Delta_V$
. Let
![]() $f_{G,z}(x, {\textrm{d}} y)$
be the probability that x is taken into a small element
$f_{G,z}(x, {\textrm{d}} y)$
be the probability that x is taken into a small element
![]() ${\textrm{d}} y \subseteq \Delta_V$
, conditioned on the event that the moves are performed on T and according to the sequence
${\textrm{d}} y \subseteq \Delta_V$
, conditioned on the event that the moves are performed on T and according to the sequence
![]() $t_{G, z}(x, y)$
. Call this event M(y). Clearly, for Lebesgue a.e. y,
$t_{G, z}(x, y)$
. Call this event M(y). Clearly, for Lebesgue a.e. y,
Let
![]() $A \subseteq \Delta_V$
be a set with
$A \subseteq \Delta_V$
be a set with
![]() $\textrm{Leb} _{m-1} (A)> 0$
. On one hand we have
$\textrm{Leb} _{m-1} (A)> 0$
. On one hand we have
On the other hand, with the notation of the above theorem, we have
 \begin{align*} & f_{G,z}(x, {\textrm{d}} y_1, {\textrm{d}} y_2, \ldots, {\textrm{d}} y_{m-1})\\[5pt] &\quad = \textbf{1}_{x_v > y_v} \dfrac{{\textrm{d}} y_v}{x_v}f_{G \setminus\{v\}, 1-y_v} \bigl(x', {\textrm{d}} y'_{\!\!1}, {\textrm{d}} y'_{\!\!2}, \ldots, {\textrm{d}} y'_{\!\!m}\bigr) \\[5pt] &\quad \quad + \textbf{1}_{x_v \le y_v} f_{G \setminus\{v\}, 1-x_v} \bigl(x', {\textrm{d}} y''_{\!\!\!1}, {\textrm{d}} y''_{\!\!\!2}, \ldots, {\textrm{d}} y''_{\!\!\!m}\bigr)\dfrac{{\textrm{d}} y_v}{y_u+y_v-x_v}.\end{align*}
\begin{align*} & f_{G,z}(x, {\textrm{d}} y_1, {\textrm{d}} y_2, \ldots, {\textrm{d}} y_{m-1})\\[5pt] &\quad = \textbf{1}_{x_v > y_v} \dfrac{{\textrm{d}} y_v}{x_v}f_{G \setminus\{v\}, 1-y_v} \bigl(x', {\textrm{d}} y'_{\!\!1}, {\textrm{d}} y'_{\!\!2}, \ldots, {\textrm{d}} y'_{\!\!m}\bigr) \\[5pt] &\quad \quad + \textbf{1}_{x_v \le y_v} f_{G \setminus\{v\}, 1-x_v} \bigl(x', {\textrm{d}} y''_{\!\!\!1}, {\textrm{d}} y''_{\!\!\!2}, \ldots, {\textrm{d}} y''_{\!\!\!m}\bigr)\dfrac{{\textrm{d}} y_v}{y_u+y_v-x_v}.\end{align*}
By the induction hypothesis, both
and
have a density with respect to the measures
![]() ${\textrm{d}} y'_{\!\!1} {\textrm{d}} y'_{\!\!2}\ldots {\textrm{d}} y'_{\!\!m}$
and
${\textrm{d}} y'_{\!\!1} {\textrm{d}} y'_{\!\!2}\ldots {\textrm{d}} y'_{\!\!m}$
and
![]() ${\textrm{d}} y''_{\!\!\!1} {\textrm{d}} y''_{\!\!\!2}\ldots {\textrm{d}} y''_{\!\!\!m}$
, respectively (all the indices but v are present). On the other hand, both measures
${\textrm{d}} y''_{\!\!\!1} {\textrm{d}} y''_{\!\!\!2}\ldots {\textrm{d}} y''_{\!\!\!m}$
, respectively (all the indices but v are present). On the other hand, both measures
![]() ${\textrm{d}} y'_{\!\!\!1} {\textrm{d}} y'_{\!\!2}\ldots {\textrm{d}} y'_{\!\!m}$
and
${\textrm{d}} y'_{\!\!\!1} {\textrm{d}} y'_{\!\!2}\ldots {\textrm{d}} y'_{\!\!m}$
and
![]() ${\textrm{d}} y''_{\!\!\!1} {\textrm{d}} y''_{\!\!\!2}\ldots {\textrm{d}} y''_{\!\!\!m}$
are the image of
${\textrm{d}} y''_{\!\!\!1} {\textrm{d}} y''_{\!\!\!2}\ldots {\textrm{d}} y''_{\!\!\!m}$
are the image of
![]() ${\textrm{d}} y_1{\textrm{d}} y_2\ldots {\textrm{d}} y_m$
(again, all the indices but v are present) under linear a.s. non-singular transformations, and thus have a density with respect to this measure. We have proved that
${\textrm{d}} y_1{\textrm{d}} y_2\ldots {\textrm{d}} y_m$
(again, all the indices but v are present) under linear a.s. non-singular transformations, and thus have a density with respect to this measure. We have proved that
![]() $f_{G, 1} (x,\cdot)$
has a density with respect to
$f_{G, 1} (x,\cdot)$
has a density with respect to
![]() $\textrm{Leb} _{m-1}$
. The following result is an immediate consequence.
$\textrm{Leb} _{m-1}$
. The following result is an immediate consequence.
Theorem 5. For every
![]() $A \subseteq \Delta_V$
with
$A \subseteq \Delta_V$
with
![]() $\textrm{Leb} _{m-1}(A)> 0$
, we have
$\textrm{Leb} _{m-1}(A)> 0$
, we have
In particular, the chain is
![]() $\textrm{Leb} _{m-1}$
-irreducible, that is, if
$\textrm{Leb} _{m-1}$
-irreducible, that is, if
![]() $\tau_A$
is the first hitting time of the chain to the set A, then
$\tau_A$
is the first hitting time of the chain to the set A, then
We have all the ingredients to prove the following theorem.
Theorem 6. There exists a unique invariant measure M for the chain
![]() $(\mu_n\colon n \ge 0)$
, and for
$(\mu_n\colon n \ge 0)$
, and for
![]() $\textrm{Leb} _{m-1}$
a.e.
$\textrm{Leb} _{m-1}$
a.e.
![]() $x \in \Delta_V$
we have
$x \in \Delta_V$
we have
where
![]() $\Vert \!\cdot\!\Vert_{\textit{TV}}$
denotes the total variation norm.
$\Vert \!\cdot\!\Vert_{\textit{TV}}$
denotes the total variation norm.
Proof. Let M be any invariant measure whose existence is guaranteed by Corollary 1. By the above theorem, P is
![]() $\textrm{Leb} _{m-1}$
-irreducible, and thus by Lemma 3 of [Reference Rosenthal12] we have
$\textrm{Leb} _{m-1}$
-irreducible, and thus by Lemma 3 of [Reference Rosenthal12] we have
![]() $\textrm{Leb} _{m-1} \ll M$
. Since the chain is obviously aperiodic, by application of the above theorem and Theorem 1 of [Reference Rosenthal12], we obtain that for
$\textrm{Leb} _{m-1} \ll M$
. Since the chain is obviously aperiodic, by application of the above theorem and Theorem 1 of [Reference Rosenthal12], we obtain that for
![]() $\textrm{Leb} _{m-1}$
a.e.
$\textrm{Leb} _{m-1}$
a.e.
![]() $x \in \Delta_V$
,
$x \in \Delta_V$
,
On the other hand, since any invariant measure for P is invariant for
![]() $P^{m-1}$
, the computation at the end of the last proof shows that every invariant measure has a density with respect to Lebesgue measure. In particular, any ergodic measure is equivalent to Lebesgue measure. Since two distinct ergodic measures must be mutually singular, this shows that M is the unique invariant measure for P.
$P^{m-1}$
, the computation at the end of the last proof shows that every invariant measure has a density with respect to Lebesgue measure. In particular, any ergodic measure is equivalent to Lebesgue measure. Since two distinct ergodic measures must be mutually singular, this shows that M is the unique invariant measure for P.![]()
5. Identification of the invariant law
For every
![]() $i \in \{1, 2, \ldots, m\}$
, set
$i \in \{1, 2, \ldots, m\}$
, set
Also, let Q be the Q-matrix associated with the continuous-time random walk on G whose jump rate from state i to state j is
![]() $p_{ij}$
. Recall that we are still under the running hypothesis that G is strongly connected, and thus the random walk associated with Q admits a unique stationary distribution, say
$p_{ij}$
. Recall that we are still under the running hypothesis that G is strongly connected, and thus the random walk associated with Q admits a unique stationary distribution, say
![]() $\nu\;:\!=\; (\nu_i)_{i=1, \ldots, m}$
.
$\nu\;:\!=\; (\nu_i)_{i=1, \ldots, m}$
.
Theorem 7. Let M be the unique invariant distribution for P. Then
Proof. We start from equation (3). To simplify notation, we write
![]() $Z_{k}= \mu^{(k)}$
. For fixed
$Z_{k}= \mu^{(k)}$
. For fixed
![]() $k\in \{1, 2, \ldots, m\}$
and
$k\in \{1, 2, \ldots, m\}$
and
![]() $t \in \mathbb{R}$
, apply (3) to the function
$t \in \mathbb{R}$
, apply (3) to the function
![]() $f\colon V \mapsto \mathbb{R}$
given by
$f\colon V \mapsto \mathbb{R}$
given by
![]() $f(i)=0$
for
$f(i)=0$
for
![]() $i \neq k$
,
$i \neq k$
,
![]() $f(k)=t$
. Then integrate both sides with respect to the invariant measure M to obtain
$f(k)=t$
. Then integrate both sides with respect to the invariant measure M to obtain
 \begin{align*} \mathbb{E}_{M} ({\textrm{e}}^{Z_k t}) & = \mathbb{E}_{M} \Biggl( {\textrm{e}}^{Z_k t } \sum_{i\neq k}\sum_{j \neq i, j \neq k}p_{ij} + \biggl[ \dfrac{{\textrm{e}}^{Z_K t}-1}{Z_k t} \biggr]p^{\textrm{out}}_{k} + \sum_{i \neq k} p_{ik}\biggl[ \dfrac{{\textrm{e}}^{(Z_i+Z_k)t}- {\textrm{e}}^{Z_k t}}{Z_i t} \biggr] \Biggr) \\[5pt] &= \mathbb{E}_{M} \Biggl( {\textrm{e}}^{Z_k t } \biggl[ 1- p_{k}^{\textrm{out}}-p_{k}^{\textrm{in}}\biggr] + \biggl[ \dfrac{{\textrm{e}}^{Z_K t}-1}{Z_k t} \biggr]p^{\textrm{out}}_{k} + \sum_{i \neq k} p_{ik} \biggl[ \dfrac{{\textrm{e}}^{(Z_i+Z_k)t}- {\textrm{e}}^{Z_k t}}{Z_i t} \biggr] \Biggr).\end{align*}
\begin{align*} \mathbb{E}_{M} ({\textrm{e}}^{Z_k t}) & = \mathbb{E}_{M} \Biggl( {\textrm{e}}^{Z_k t } \sum_{i\neq k}\sum_{j \neq i, j \neq k}p_{ij} + \biggl[ \dfrac{{\textrm{e}}^{Z_K t}-1}{Z_k t} \biggr]p^{\textrm{out}}_{k} + \sum_{i \neq k} p_{ik}\biggl[ \dfrac{{\textrm{e}}^{(Z_i+Z_k)t}- {\textrm{e}}^{Z_k t}}{Z_i t} \biggr] \Biggr) \\[5pt] &= \mathbb{E}_{M} \Biggl( {\textrm{e}}^{Z_k t } \biggl[ 1- p_{k}^{\textrm{out}}-p_{k}^{\textrm{in}}\biggr] + \biggl[ \dfrac{{\textrm{e}}^{Z_K t}-1}{Z_k t} \biggr]p^{\textrm{out}}_{k} + \sum_{i \neq k} p_{ik} \biggl[ \dfrac{{\textrm{e}}^{(Z_i+Z_k)t}- {\textrm{e}}^{Z_k t}}{Z_i t} \biggr] \Biggr).\end{align*}
Differentiate with respect to t on both sides. By virtue of the Lebesgue-dominated convergence theorem, after evaluation at
![]() $t=0$
we obtain
$t=0$
we obtain
and this yields
which is equation (7).![]()
After Proposition 2, intuition dictates that in the case
![]() $m \ge 2$
, the invariant probability measure should be related in some way to the Dirichlet distribution. Indeed, this educated guess is exactly right in at least one simple case. For the rest of this paper, we will need the following condition to hold.
$m \ge 2$
, the invariant probability measure should be related in some way to the Dirichlet distribution. Indeed, this educated guess is exactly right in at least one simple case. For the rest of this paper, we will need the following condition to hold.
Assumption 2. The transport probabilities are symmetric, namely
Let M
′ be the symmetric
![]() $1/2$
-Dirichlet distribution. Assume that
$1/2$
-Dirichlet distribution. Assume that
![]() $X=(X_1, X_2, \ldots, X_m) \sim M'$
. It is well known that for any multi-index with positive integer components
$X=(X_1, X_2, \ldots, X_m) \sim M'$
. It is well known that for any multi-index with positive integer components
![]() $\beta=(\beta_1, \ldots, \beta_m)$
, we have
$\beta=(\beta_1, \ldots, \beta_m)$
, we have
 \begin{align} \mathbb{E} \bigl( X^\beta \bigr) & = \mathbb{E} \Biggl( \prod_{i=1}^m X_i^{\beta_i} \Biggr) = \dfrac{\Gamma ( m/2 ) }{\Gamma (1/2)^m \Gamma \bigl(m/2+ \sum _{i=1}^m \beta_i \bigr)} \prod_{i=1}^m \Gamma ( \beta_i + 1/2).\end{align}
\begin{align} \mathbb{E} \bigl( X^\beta \bigr) & = \mathbb{E} \Biggl( \prod_{i=1}^m X_i^{\beta_i} \Biggr) = \dfrac{\Gamma ( m/2 ) }{\Gamma (1/2)^m \Gamma \bigl(m/2+ \sum _{i=1}^m \beta_i \bigr)} \prod_{i=1}^m \Gamma ( \beta_i + 1/2).\end{align}
Let U be a
![]() $\operatorname{Uniform}[0,1]$
random variable independent of X. The action of the semigroup of the process
$\operatorname{Uniform}[0,1]$
random variable independent of X. The action of the semigroup of the process
![]() $(\mu_n\colon n \ge 0)$
on the monomials
$(\mu_n\colon n \ge 0)$
on the monomials
when the initial distribution is M ′ can be written as
 \begin{align}M'Pf = \sum_{ij \in E} p_{ij} \mathbb{E} \Biggl( (X_i(1-U))^{\beta_i}(X_j+UX_i)^{\beta_j} \prod_{r\neq i, j} X_r^{\beta_r} \Biggr).\end{align}
\begin{align}M'Pf = \sum_{ij \in E} p_{ij} \mathbb{E} \Biggl( (X_i(1-U))^{\beta_i}(X_j+UX_i)^{\beta_j} \prod_{r\neq i, j} X_r^{\beta_r} \Biggr).\end{align}
Let
![]() $S_{ij}$
be the general term of the sum above. Plainly
$S_{ij}$
be the general term of the sum above. Plainly
 \begin{align*}S_{ij}&=p_{ij} \mathbb{E} \Biggl( (X_i(1-U))^{\beta_i}(X_j+UX_i)^{\beta_j} \prod_{r\neq i, j} X_r^{\beta_r} \Biggr) \\[5pt] & = p_{ij} \sum_{k=0}^{\beta_j} \binom{\beta_j}{k} \mathbb{E} \Biggl( (1-U)^{\beta_i} U^k X_i^{\beta_i} X_j^{\beta_j-k}X_i^k \prod_{r\neq i, j} X_r^{\beta_r} \Biggr)\\[5pt] & = p_{ij} \sum_{k=0}^{\beta_j} \binom{\beta_j}{k} \mathbb{E} \bigl( (1-U)^{\beta_i} U^k\bigr) \mathbb{E} \Biggl( X_i^{\beta_i+k} X_j^{\beta_j-k} \prod_{r\neq i, j} X_r^{\beta_r} \Biggr),\end{align*}
\begin{align*}S_{ij}&=p_{ij} \mathbb{E} \Biggl( (X_i(1-U))^{\beta_i}(X_j+UX_i)^{\beta_j} \prod_{r\neq i, j} X_r^{\beta_r} \Biggr) \\[5pt] & = p_{ij} \sum_{k=0}^{\beta_j} \binom{\beta_j}{k} \mathbb{E} \Biggl( (1-U)^{\beta_i} U^k X_i^{\beta_i} X_j^{\beta_j-k}X_i^k \prod_{r\neq i, j} X_r^{\beta_r} \Biggr)\\[5pt] & = p_{ij} \sum_{k=0}^{\beta_j} \binom{\beta_j}{k} \mathbb{E} \bigl( (1-U)^{\beta_i} U^k\bigr) \mathbb{E} \Biggl( X_i^{\beta_i+k} X_j^{\beta_j-k} \prod_{r\neq i, j} X_r^{\beta_r} \Biggr),\end{align*}
where the last line follows from the independence between X and U. On the one hand,
On the other hand, by (8),
 \begin{align*}\mathbb{E} \Biggl( X_i^{\beta_i+k} X_j^{\beta_j-k} \prod_{r\neq i, j} X_r^{\beta_r} \Biggr) & = \dfrac{\Gamma ( m/2 ) \Gamma (\beta_i+k+1/2)\Gamma (\beta_j-k+1/2)}{\Gamma (1/2)^m \Gamma \bigl(m/2+ \sum _{s=1}^m \beta_s \bigr)}\prod_{r\neq i,j} \Gamma ( \beta_r + 1/2).\end{align*}
\begin{align*}\mathbb{E} \Biggl( X_i^{\beta_i+k} X_j^{\beta_j-k} \prod_{r\neq i, j} X_r^{\beta_r} \Biggr) & = \dfrac{\Gamma ( m/2 ) \Gamma (\beta_i+k+1/2)\Gamma (\beta_j-k+1/2)}{\Gamma (1/2)^m \Gamma \bigl(m/2+ \sum _{s=1}^m \beta_s \bigr)}\prod_{r\neq i,j} \Gamma ( \beta_r + 1/2).\end{align*}
Thus
 \begin{align}S_{ij}& =p_{ij} \dfrac{\Gamma (m/2)}{\Gamma (1/2)^m \Gamma \bigl(m/2+ \sum _{s=1}^m \beta_s \bigr) } \prod_{r\neq i,j} \Gamma ( \beta_r + 1/2) \nonumber \\[5pt] & \quad \times \sum_{k=0}^{\beta_j} \biggl( \dfrac{\Gamma (\beta_i+1)\Gamma (\beta_i+k+1/2) }{\Gamma (\beta_i+k+2)} \dfrac{\Gamma (\beta_j+1)\Gamma (\beta_j-k+1/2) }{\Gamma (\beta_j-k+1)} \biggr) \nonumber \\[5pt] & = p_{ij} Mf \dfrac{\Gamma (\beta_i+1) \Gamma (\beta_j+1)}{\Gamma (\beta_i+1/2) \Gamma (\beta_j+1/2)}\nonumber \\[5pt] & \quad \times \sum_{k=0}^{\beta_j} \biggl( \dfrac{\Gamma (\beta_i+k+1/2) }{\Gamma (\beta_i+k+2)} \dfrac{\Gamma (\beta_j-k+1/2) }{\Gamma (\beta_j-k+1)} \biggr).\end{align}
\begin{align}S_{ij}& =p_{ij} \dfrac{\Gamma (m/2)}{\Gamma (1/2)^m \Gamma \bigl(m/2+ \sum _{s=1}^m \beta_s \bigr) } \prod_{r\neq i,j} \Gamma ( \beta_r + 1/2) \nonumber \\[5pt] & \quad \times \sum_{k=0}^{\beta_j} \biggl( \dfrac{\Gamma (\beta_i+1)\Gamma (\beta_i+k+1/2) }{\Gamma (\beta_i+k+2)} \dfrac{\Gamma (\beta_j+1)\Gamma (\beta_j-k+1/2) }{\Gamma (\beta_j-k+1)} \biggr) \nonumber \\[5pt] & = p_{ij} Mf \dfrac{\Gamma (\beta_i+1) \Gamma (\beta_j+1)}{\Gamma (\beta_i+1/2) \Gamma (\beta_j+1/2)}\nonumber \\[5pt] & \quad \times \sum_{k=0}^{\beta_j} \biggl( \dfrac{\Gamma (\beta_i+k+1/2) }{\Gamma (\beta_i+k+2)} \dfrac{\Gamma (\beta_j-k+1/2) }{\Gamma (\beta_j-k+1)} \biggr).\end{align}
For a, b non-negative integer numbers, define
 \begin{align*} R(a, b)\;:\!=\; \dfrac{\Gamma (a+1) \Gamma (b+1)}{\Gamma (a+1/2) \Gamma (b+1/2)} \sum_{k=0}^{b} \biggl( \dfrac{\Gamma (a+k+1/2) }{\Gamma (a+k+2)} \dfrac{\Gamma (b-k+1/2) }{\Gamma (b-k+1)} \biggr).\end{align*}
\begin{align*} R(a, b)\;:\!=\; \dfrac{\Gamma (a+1) \Gamma (b+1)}{\Gamma (a+1/2) \Gamma (b+1/2)} \sum_{k=0}^{b} \biggl( \dfrac{\Gamma (a+k+1/2) }{\Gamma (a+k+2)} \dfrac{\Gamma (b-k+1/2) }{\Gamma (b-k+1)} \biggr).\end{align*}
The following lemma establishes the crucial algebraic identity.
Lemma 2. For arbitrary
![]() $a, b \in \mathbb{Z}_+$
,
$a, b \in \mathbb{Z}_+$
,
Proof. A simple computation shows that
 \begin{align} R (a, b) = \dfrac{1}{a+1} {}_{3}F_{2}\left[\begin{array}{l}{1, a+\tfrac{1}{2}, -b}\\[5pt] {a+2, -b + \tfrac{1}{2}}\end{array};\,{1}\right],\end{align}
\begin{align} R (a, b) = \dfrac{1}{a+1} {}_{3}F_{2}\left[\begin{array}{l}{1, a+\tfrac{1}{2}, -b}\\[5pt] {a+2, -b + \tfrac{1}{2}}\end{array};\,{1}\right],\end{align}
where
![]() ${}_3F_2[\ ;\,]$
is the generalized (3, 2)-hypergeometric function. By the classic Pfaff–Saalschütz theorem (see [Reference Slater13, pages 48--49]), we have
${}_3F_2[\ ;\,]$
is the generalized (3, 2)-hypergeometric function. By the classic Pfaff–Saalschütz theorem (see [Reference Slater13, pages 48--49]), we have
 \begin{align} {}_{3}F_{2}\left[\begin{array}{l}{1, a+\tfrac{1}{2}, -b}\\[5pt] {a+2, -b + \tfrac{1}{2}}\end{array};\,{1}\right] = \tfrac{ {(a+1)}_{b} \bigl(\tfrac{3}{2}\bigr)_{b}}{{(a+2)}_{b} \bigl(\tfrac{1}{2}\bigr)_{b}},\end{align}
\begin{align} {}_{3}F_{2}\left[\begin{array}{l}{1, a+\tfrac{1}{2}, -b}\\[5pt] {a+2, -b + \tfrac{1}{2}}\end{array};\,{1}\right] = \tfrac{ {(a+1)}_{b} \bigl(\tfrac{3}{2}\bigr)_{b}}{{(a+2)}_{b} \bigl(\tfrac{1}{2}\bigr)_{b}},\end{align}
where
![]() $({x})_{n}$
is the Pochhammer symbol:
$({x})_{n}$
is the Pochhammer symbol:
Substitute (12) into (11). After some simplifications, we get
and analogously
The result follows.![]()
We have the ingredients to prove our main result.
Theorem 8. Assume
![]() $(G, \textbf{p})$
satisfies Assumption 2. The unique P-invariant probability measure is the symmetric Dirichlet distribution with concentration parameter
$(G, \textbf{p})$
satisfies Assumption 2. The unique P-invariant probability measure is the symmetric Dirichlet distribution with concentration parameter
![]() $1/2$
.
$1/2$
.
Proof. By equations (9) and (10), for f a monomial, we have
 \begin{align*} M'P f& = M'f \sum_{i < j} ( p_{ij} R (\beta_i, \beta_j)+ p_{ji} R(\beta_j, \beta_i) )\\[5pt] & = M'f \sum_{i < j} ( 2 p_{ij} ) \\[5pt] &= M'f,\end{align*}
\begin{align*} M'P f& = M'f \sum_{i < j} ( p_{ij} R (\beta_i, \beta_j)+ p_{ji} R(\beta_j, \beta_i) )\\[5pt] & = M'f \sum_{i < j} ( 2 p_{ij} ) \\[5pt] &= M'f,\end{align*}
where the last line follows from Assumption 2. By finite additivity, the result is still true for polynomials. Since the class of polynomials is a point-separating algebra of continuous functions on
![]() $\Delta_V$
, which is a Polish space, in [Reference Ethier and Kurtz4, Theorem 3.4.5, a)], we conclude that
$\Delta_V$
, which is a Polish space, in [Reference Ethier and Kurtz4, Theorem 3.4.5, a)], we conclude that
on
![]() $\mathcal{B}(\Delta_V)$
. By Theorem 6,
$\mathcal{B}(\Delta_V)$
. By Theorem 6,
![]() $M'=M$
, the unique probability measure for P.
$M'=M$
, the unique probability measure for P.![]()
6. Final remarks
We finish this article with two simple remarks that, although not connected with the general topic of this paper, show interesting possibilities for further study.
First, the process just described is, in some sense, related to the well-known averaging process (AP: see the beautiful survey by Aldous and Lanoue [Reference Aldous and Lanoue1] for a simple description). Remember some easy facts about the AP. Given a finite connected graph
![]() $G=(V, E)$
, we attach to every (undirected) edge
$G=(V, E)$
, we attach to every (undirected) edge
![]() $e \in E$
a Poisson process
$e \in E$
a Poisson process
![]() $N_e$
of intensity
$N_e$
of intensity
![]() $\nu_e$
. Initially, a real number
$\nu_e$
. Initially, a real number
![]() $X_v (0)$
is given to every vertex
$X_v (0)$
is given to every vertex
![]() $v \in V$
. The AP is the continuous-time Markov chain
$v \in V$
. The AP is the continuous-time Markov chain
![]() $(X_u(t)\colon u \in V, t \ge 0)$
with state-space
$(X_u(t)\colon u \in V, t \ge 0)$
with state-space
![]() $\mathbb{R}^V$
that evolves according to the following rule: when the process
$\mathbb{R}^V$
that evolves according to the following rule: when the process
![]() $N_e$
jumps, say at time T, then we update the values of the incident vertices at e averaging their values at time
$N_e$
jumps, say at time T, then we update the values of the incident vertices at e averaging their values at time
![]() $T-$
. More precisely, if
$T-$
. More precisely, if
![]() $e=\{u,v\}$
, we perform the change
$e=\{u,v\}$
, we perform the change
If the initial values are positive numbers adding up to 1, then the AP can be seen as a
![]() $\Delta_V$
-valued Markov process. It can be proved that the unique invariant probability measure for this process is the point mass at the Uniform distribution on V. Let Q be the generator of the continuous time random walk with rates
$\Delta_V$
-valued Markov process. It can be proved that the unique invariant probability measure for this process is the point mass at the Uniform distribution on V. Let Q be the generator of the continuous time random walk with rates
![]() $\nu_{(i,j)}= \nu_{(j,i)}= \nu _{\{i,j\}}$
. It is straightforward to show that the averages obey the ODE
$\nu_{(i,j)}= \nu_{(j,i)}= \nu _{\{i,j\}}$
. It is straightforward to show that the averages obey the ODE
Now the process
![]() $(\mu_n\colon n \ge 0)$
that we have studied in this paper can be put into the setting of a continuous-time process as follows. To every directed edge
$(\mu_n\colon n \ge 0)$
that we have studied in this paper can be put into the setting of a continuous-time process as follows. To every directed edge
![]() $e=(u,v)$
of G, attach a Poisson process
$e=(u,v)$
of G, attach a Poisson process
![]() $N_e$
of rate
$N_e$
of rate
![]() $p_{uv}$
. When the process
$p_{uv}$
. When the process
![]() $N_{(u,v)}$
jumps, transport a uniformly chosen chunk of mass from u to v. Observe that with this prescription for the jump rate of
$N_{(u,v)}$
jumps, transport a uniformly chosen chunk of mass from u to v. Observe that with this prescription for the jump rate of
![]() $\mu_t$
, the process is running at twice the speed of the Aldous–Lanoue AP. On the other hand, the reader can check that in this case the mean process
$\mu_t$
, the process is running at twice the speed of the Aldous–Lanoue AP. On the other hand, the reader can check that in this case the mean process
![]() $\mathbb{E}(\mu_t)$
obeys the same equation (13).
$\mathbb{E}(\mu_t)$
obeys the same equation (13).
Finally, it would be interesting to devise a strategy allowing us to characterize the unique invariant measure in the non-symmetric case as well. Ideally, such a characterization should be based on the corresponding invariant measure of the underlying random walk. The reader can convince herself that the steps toward the proof of Theorem 8 do not generalize to the setting where the hypothesis of symmetric rates does not hold, and thus we need other tools to achieve the goal. On the other hand, the proof provided above is purely algebraic. It would be desirable to have a probabilistic insight of our results, presumably based on an argument of the stick-breaking type.
Funding information
This research was supported by ANID through Beca de Doctorado 2017-21170406, and partially funded by project ANID-FONDECYT 1200925.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.