A direct numerical simulation (DNS) based on the lattice Boltzmann method (LBM) is carried out in low-Reynolds-number grid turbulence to analyse the mean turbulent kinetic energy dissipation rate,  $\overline{\epsilon }$, and its transport equation during decay. All the components of
$\overline{\epsilon }$, and its transport equation during decay. All the components of  $\overline{\epsilon }$ and its transport equation terms are computed, providing for the first time the opportunity to assess the contribution of each term to the decay. The results indicate that although small departures from isotropy are observed in the components of
$\overline{\epsilon }$ and its transport equation terms are computed, providing for the first time the opportunity to assess the contribution of each term to the decay. The results indicate that although small departures from isotropy are observed in the components of  $\overline{\epsilon }$ and its destruction term, there is sufficient compensation among the components for these two quantities to satisfy isotropy to a close approximation. A short distance downstream of the grid, the transport equation of
$\overline{\epsilon }$ and its destruction term, there is sufficient compensation among the components for these two quantities to satisfy isotropy to a close approximation. A short distance downstream of the grid, the transport equation of  $\overline{\epsilon }$ simplifies to its high-Reynolds-number homogeneous and isotropic form. The decay rate of
$\overline{\epsilon }$ simplifies to its high-Reynolds-number homogeneous and isotropic form. The decay rate of  $\overline{\epsilon }$ is governed by the imbalance between the production due to vortex stretching and the destruction caused by the action of viscosity, the latter becoming larger than the former as the distance from the grid increases. This imbalance, which is not constant during the decay as argued by Batchelor & Townsend (Proc. R. Soc. Lond. A, vol. 190, 1947, pp. 534–550), varies according to a power law of
$\overline{\epsilon }$ is governed by the imbalance between the production due to vortex stretching and the destruction caused by the action of viscosity, the latter becoming larger than the former as the distance from the grid increases. This imbalance, which is not constant during the decay as argued by Batchelor & Townsend (Proc. R. Soc. Lond. A, vol. 190, 1947, pp. 534–550), varies according to a power law of  $x$, the distance downstream of the grid. The non-constancy implies a lack of dynamical similarity in the mechanisms controlling the transport of
$x$, the distance downstream of the grid. The non-constancy implies a lack of dynamical similarity in the mechanisms controlling the transport of  $\overline{\epsilon }$. This is consistent with the fact that the power-law-decay (
$\overline{\epsilon }$. This is consistent with the fact that the power-law-decay (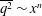 $\overline{q^2} \sim x^n$) exponent
$\overline{q^2} \sim x^n$) exponent  $n$ is not equal to
$n$ is not equal to  $-$1. It is actually close to
$-$1. It is actually close to  $-$1.6, a value in keeping with the relatively low Reynolds number of the simulation. These results highlight the importance of the imbalance in establishing the value of
$-$1.6, a value in keeping with the relatively low Reynolds number of the simulation. These results highlight the importance of the imbalance in establishing the value of  $n$. The
$n$. The  $\overline{\epsilon }$-transport equation is also analysed in relation to the power-law decay. The results show that the power-law exponent
$\overline{\epsilon }$-transport equation is also analysed in relation to the power-law decay. The results show that the power-law exponent  $n$ is controlled by the imbalance between production and destruction. Further, a relatively straightforward analysis provides information on the behaviour of
$n$ is controlled by the imbalance between production and destruction. Further, a relatively straightforward analysis provides information on the behaviour of  $n$ during the entire decay process and an interesting theoretical result, which is yet to be confirmed, when
$n$ during the entire decay process and an interesting theoretical result, which is yet to be confirmed, when 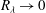 $R_{\lambda } \rightarrow 0 $, namely, the destruction coefficient
$R_{\lambda } \rightarrow 0 $, namely, the destruction coefficient 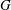 $G$ is constant and its value must lie between
$G$ is constant and its value must lie between 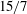 $15/7$ and
$15/7$ and 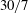 $30/7$. These two limits encompass the predictions for the final period of decay by Batchelor & Townsend (1947) and Saffman (J. Fluid Mech., vol. 27, 1967, pp. 581–593).
$30/7$. These two limits encompass the predictions for the final period of decay by Batchelor & Townsend (1947) and Saffman (J. Fluid Mech., vol. 27, 1967, pp. 581–593).
 $\kappa $
-HOMOGENEOUS, BUT NOT
$\kappa $
-HOMOGENEOUS, BUT NOT
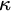 $\kappa $
-TRANSITIVE PERMUTATION GROUPS
$\kappa $
-TRANSITIVE PERMUTATION GROUPS
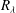 $R_{\lambda }$ grid turbulence
$R_{\lambda }$ grid turbulence