We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This journal utilises an Online Peer Review Service (OPRS) for submissions. By clicking "Continue" you will be taken to our partner site https://rse.msp.org/submit_new.php?j=rse_proc_a_math. Please be aware that your Cambridge account is not valid for this OPRS and registration is required. We strongly advise you to read all "Author instructions" in the "Journal information" area prior to submitting.
Denote by m(G) the largest size of a minimal generating set of a finite group G. We estimate m(G) in terms of 
$\sum _{p\in \pi (G)}d_p(G),$ where we are denoting by dp(G) the minimal number of generators of a Sylow p-subgroup of G and by π(G) the set of prime numbers dividing the order of G.
We prove the non-degeneracy of the extremals of the Sobolev inequality
when 1 < p < N, as solutions of a critical quasilinear equation involving the p-Laplacian.
\[ \int_{\mathbb R^N}|\nabla u|^p\,\rd x\ge \mathcal S_p\int_{\open R^N}|u|^\frac{Np}{N-p}\,\rd x,\quad u\in \mathcal D^{1,p}(\open R^N) \]
Bożejko and Speicher associated a finite von Neumann algebra MT to a self-adjoint operator T on a complex Hilbert space of the form 
$\mathcal {H}\otimes \mathcal {H}$ which satisfies the Yang–Baxter relation and 
$ \left\| T \right\| < 1$. We show that if dim
$(\mathcal {H})$ ⩾ 2, then MT is a factor when T admits an eigenvector of some special form.
A subset X of a Polish group G is Haar null if there exists a Borel probability measure μ and a Borel set B containing X such that μ(gBh) = 0 for every g, h ∈ G. A set X is Haar meager if there exists a compact metric space K, a continuous function f : K → G and a Borel set B containing X such that f−1(gBh) is meager in K for every g, h ∈ G. We calculate (in ZFC) the four cardinal invariants (add, cov, non, cof) of these two σ-ideals for the simplest non-locally compact Polish group, namely in the case 
$G = \mathbb {Z}^\omega$. In fact, most results work for separable Banach spaces as well, and many results work for Polish groups admitting a two-sided invariant metric. This answers a question of the first named author and Vidnyánszky.
First we introduce the notion of parallel Ricci tensor 
${\nabla }\mathrm {Ric}=0$ for real hypersurfaces in the complex quadric Qm = SOm+2/SOmSO2 and show that the unit normal vector field N is singular. Next we give a new classification of real hypersurfaces in the complex quadric Qm = SOm+2/SOmSO2 with parallel Ricci tensor.
In this paper, we mainly investigate two versions of the Bohr theorem for slice regular functions over the largest alternative division algebras of octonions 
$\mathbb {O}$. To this end, we establish the coefficient estimates for self-maps of the unit ball of 
$\mathbb {O}$ and the Carathéodory class in this setting. As a further application of the coefficient estimate, the 1/2-covering theorem is also proven for slice regular functions with convex image.
We study the quasilinear elliptic inequality
where 
\[ -\Delta_m u - \frac{\mu}{|x|^m}u^{m-1} \geq (I_\alpha*u^p)u^q \quad\mbox{in }\mathbb{R}^N\setminus \overline B_1, N\geq 1, \]
$p>0$, 
$q, \mu \in \mathbb {R}$, 
$m>1$ and 
$I_\alpha$ is the Riesz potential of order 
$\alpha \in (0,N)$. We obtain necessary and sufficient conditions for the existence of positive solutions.
We study the existence and concentration of positive solutions for the following class of fractional p-Kirchhoff type problems:
where ɛ is a small positive parameter, a and b are positive constants, s ∈ (0, 1) and p ∈ (1, ∞) are such that 
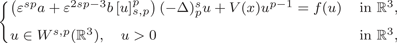$$ \left\{\begin{array}{@{}ll} \left(\varepsilon^{sp}a+\varepsilon^{2sp-3}b \,[u]_{s, p}^{p}\right)(-\Delta)_{p}^{s}u+V(x)u^{p-1}=f(u) & \text{in}\ \mathbb{R}^{3},\\ \noalign{ u\in W^{s, p}(\mathbb{R}^{3}), \quad u>0 & \text{in}\ \mathbb{R}^{3}, \end{array}\right.$$
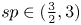$sp \in (\frac {3}{2}, 3)$, 
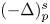$(-\Delta )^{s}_{p}$ is the fractional p-Laplacian operator, f: ℝ → ℝ is a superlinear continuous function with subcritical growth and V: ℝ3 → ℝ is a continuous potential having a local minimum. We also prove a multiplicity result and relate the number of positive solutions with the topology of the set where the potential V attains its minimum values. Finally, we obtain an existence result when f(u) = uq−1 + γur−1, where γ > 0 is sufficiently small, and the powers q and r satisfy 2p < q < p*s ⩽ r. The main results are obtained by using some appropriate variational arguments.
A directed space is a topological space 
$X$ together with a subspace 
$\vec {P}(X)\subset X^I$ of directed paths on 
$X$. A symmetry of a directed space should therefore respect both the topology of the underlying space and the topology of the associated spaces 
$\vec {P}(X)_-^+$ of directed paths between a source (
$-$) and a target (
$+$)—up to homotopy. If it is, moreover, homotopic to the identity map—in a directed sense—such a symmetry will be called an inessential d-map, and the paper explores the algebra and topology of inessential d-maps. Comparing two d-spaces 
$X$ and 
$Y$ ‘up to symmetry’ yields the notion of a directed homotopy equivalence between them. Under appropriate conditions, all directed homotopy equivalences are shown to satisfy a 2-out-of-3 property. Our notion of directed homotopy equivalence does not agree completely with the one defined in Goubault (2017, arxiv:1709:05702v2) and Goubault, Farber and Sagnier (2020, J. Appl. Comput. Topol. 4, 11–27); the deviation is motivated by examples. Nevertheless, directed topological complexity, introduced in Goubault, Farber and Sagnier (2020) is shown to be invariant under our notion of directed homotopy equivalence. Finally, we show that directed homotopy equivalences result in isomorphisms on the pair component categories of directed spaces introduced in Goubault, Farber and Sagnier (2020).