By a formula of Farber, the topological complexity TC(X) of a (p − 1)-connected m-dimensional CW-complex X is bounded above by (2m + 1)/p + 1. We show that the same result holds for the monoidal topological complexity TCM(X). In a previous paper we introduced various lower bounds for TCM(X), such as the nilpotency of the ring H*(X × X, Δ(X)), and the weak and stable (monoidal) topological complexity wTCM(X) and σTCM(X). In general, the difference between these upper and lower bounds can be arbitrarily large. In this paper we investigate spaces with topological complexity close to the maximal value given by Farber's formula. We show that in these cases the gap between the lower and upper bounds is narrow and TC(X) often coincides with the lower bounds.

Let (X, d, μ) be a metric measure space and let it satisfy the so-called upper doubling condition and the geometrically doubling condition. We show that, for the maximal Calderón–Zygmund operator associated with a singular integral whose kernel satisfies the standard size condition and the Hörmander condition, its Lp(μ)-boundedness with p ∈ (1, ∞) is equivalent to its boundedness from L1(μ) into L1,∞(μ). Moreover, applying this, together with a new Cotlar-type inequality, the authors show that if the Calderón–Zygmund operator T is bounded on L2(μ), then the corresponding maximal Calderón–Zygmund operator is bounded on Lp(μ) for all p ∈ (1, ∞), and bounded from L1(μ) into L1,∞ (μ). These results essentially improve the existing results.

We study the radial symmetry of large solutions of the semilinear elliptic problem Δu + ∇h · ∇u = f (∣x∣, u), and we provide sharp conditions under which the problem has a radial solution. The result is independent of the rate of growth of the solution at infinity.

For Banach spaces X and Y, we consider bifurcation from the line of trivial solutions for the equation F (λ, u) = 0, where F : ℝ × X → Y with F (λ, 0) = 0 for all λ ∈ ℝ. The focus is on the situation where F (λ, ·) is only Hadamard differentiable at 0 and Lipschitz continuous on some open neighbourhood of 0, without requiring any Fréchet differentiability. Applications of the results obtained here to some problems involving nonlinear elliptic equations on ℝN, where Fréchet differentiability is not available, are presented in some related papers, which shed light on the relevance of our hypotheses.

In this paper, we consider the Cauchy problem for an inviscid two-phase gas—liquid model with external force, in order to demonstrate the smoothing effect on the damping mechanism. It is shown that the Cauchy problem admits a unique global smooth solution provided that the initial data are smooth and the C0-norm of the derivative of the initial data are small.

We deal with the optimal control of systems driven by differential inclusions with anti-periodic conditions in Banach spaces. The operators in the differential inclusions, describing the control system, all depend on control variables. By a solution of the control system we mean a ‘trajectory-control’ pair. We first prove that, for fixed control variables, the set of solutions is non-empty for the corresponding differential inclusion with anti-periodic conditions. We then show the functional-topological properties of the set of solutions. Finally, we investigate the existence of solutions to the optimal control problem. These abstract results can be used to study optimal control systems of evolutionary hemi-variational inequalities.

We study steady periodic water waves with variable vorticity and density, where we allow for stagnation points in the flow, and where we admit the capillarity effects of surface tension. Using global bifurcation theory, we extend a local curve of non-trivial solutions of the governing equations to a global continuum of solutions. Furthermore, we obtain a description of the behaviour of the solutions along this continuum.

We consider semilinear evolution equations for which the linear part is normal and generates a strongly continuous semigroup, and the nonlinear part is sufficiently smooth on a scale of Hilbert spaces. We approximate their semi-flow by an implicit A-stable Runge–Kutta discretization in time and a spectral Galerkin truncation in space. We show regularity of the Galerkin-truncated semi-flow and its time discretization on open sets of initial values with bounds that are uniform in the spatial resolution and the initial value. We also prove convergence of the space-time discretization without any condition that couples the time step to the spatial resolution. We then estimate the Galerkin truncation error for the semi-flow of the evolution equation, its Runge–Kutta discretization and their respective derivatives, showing how the order of the Galerkin truncation error depends on the smoothness of the initial data. Our results apply, in particular, to the semilinear wave equation and to the nonlinear Schrodinger equation.

The aim of this paper is to show that the p-local homotopy type of the gauge group of a principal bundle over an even-dimensional sphere is completely determined by the divisibility of the classifying map by p. In particular, for gauge groups of principal SU(n)-bundles over S2d for 2 ≤ d ≤ p − 1 and n ≤ 2p − 1, we give a concrete classification of their p-local homotopy types.

This paper deals with the coupled chemotaxis-haptotaxis model of cancer invasion given by

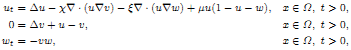
where χ, ξ and μ are positive parameters and Ω ⊂ ℝn (n ≥ 1) is a bounded domain with smooth boundary. Under zero-flux boundary conditions, it is shown that, for any μ > χ and any sufficiently smooth initial data (u0, w0) satisfying u0 ≥ 0 and w0 > 0, the associated initial–boundary-value problem possesses a unique global smooth solution that is uniformly bounded. Moreover, we analyse the stability and attractivity properties of the non-trivial homogeneous equilibrium (u, v, w) ≡ (1,1, 0) and establish a quantitative result relating the domain of attraction of this steady state to the size of μ. In particular, this will imply that whenever u0 > 0 and 0 < w0 < 1 in 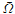there exists a positive constant μ* depending only on χ, ξ, Ω, u0 and w0 such that for any μ < μ* the above global solution (u, v, w) approaches the spatially uniform state (1, 1, 0) as time goes to infinity.

We study the boundary-value problem ũt = Δxũ(x,t), ũ(x, 0) = u(x), where x ∈ Ω, t ∈ (0,T), Ω ⊆ ℝn−1 is a bounded Lipschitz boundary domain, u belongs to a certain Orlicz–Slobodetskii space YR,R(Ω). Under certain assumptions on the Orlicz function R, we prove that the solution u belongs to the Orlicz–Sobolev space W1,R(Ω × (0,T)).

This paper is devoted to the study of a typical (p, q)-gradient elliptic system. We discuss the existence of multiple non-trivial solutions. More precisely, we establish the existence of three non-trivial solutions, obtained by applying the fibering method introduced by Pohozaev.

In this paper, we consider the semilinear elliptic equation −Δu = λf(x,u) with the Dirichlet boundary value, and under suitable assumptions on the nonlinear term f with a more general growth condition. Some existence results of solutions are given for all λ > 0 via the variational method and some analysis techniques.

We study the weighted p-Laplacian with an isolated singular point, and discuss some properties of solutions near such a point, including removable singularities, boundedness and growth rate estimates. In particular, some relevant critical exponents are exactly determined.

We consider the fractional derivative of a general Poisson semigroup. With this fractional derivative, we define the generalized fractional Littlewood–Paley g-function for semigroups acting on Lp-spaces of functions with values in Banach spaces. We give a characterization of the classes of Banach spaces for which the fractional Littlewood–Paley g-function is bounded on Lp-spaces. We show that the class of Banach spaces is independent of the order of derivation and coincides with the classical (Lusin-type/-cotype) case. We also show that the same kind of results exist for the case of the fractional area function and the fractional gλ*-function on ℝn. Finally, we consider the relationship of the almost sure finiteness of the fractional Littlewood–Paley g-function, the area function and the gλ*-function with the Lusin-cotype property of the underlying Banach space. As a byproduct of the techniques developed, one can find some results of independent interest for vector-valued Calderón–Zygmund operators. For example, one can find the following characterization: a Banach space is the unconditional martingale difference if and only if, for some (or, equivalently, for every) p ∈ [1, ∞), dy exists for almost every x ∈ ℝ and every .

In this paper, the bond-based peridynamic system is analysed as a non-local boundary-value problem with volume constraint. The study extends earlier works in the literature on non-local diffusion and non-local peridynamic models, to include non-positive definite kernels. We prove the well-posedness of both linear and nonlinear variational problems with volume constraints. The analysis is based on some non-local Poincaré-type inequalities and the compactness of the associated non-local operators. It also offers careful characterizations of the associated solution spaces, such as compact embedding, separability and completeness. In the limit of vanishing non-locality, the convergence of the peridynamic system to the classical Navier equations of elasticity with Poisson ratio ¼ is demonstrated.

We are interested in finding the entire solutions of non-quasi-monotone delayed non-local reaction–diffusion equations. It is well known that the comparison principle is not applicable for such equations. To overcome this difficulty, we introduce two auxiliary quasi-monotone equations and establish some comparison arguments for the three systems. Some new types of entire solutions are then constructed using the comparison argument, the travelling wavefronts and a spatially independent solution of the auxiliary equations. We also extend our arguments to a delayed cellular neural network with non-monotonic output functions and a delayed non-local lattice differential equation with non-monotonic birth functions.

Employing the Kolodner–Coffman method, we show the exact multiplicity of positive solutions for the one-dimensional p-Laplacian that is subject to a Dirichlet boundary condition with a positive convex nonlinearity and an indefinite weight function.

In this paper, we revisit a reaction—diffusion autocatalytic chemical reaction model with decay. For higher-order reactions, we prove that the system possesses at least two positive steady-state solutions; hence, it has bistable dynamics similar to the system without decay. For the linear reaction, we determine the necessary and sufficient condition to ensure the existence of a solution. Moreover, in the one-dimensional case, we prove that the positive steady-state solution is unique. Our results demonstrate the drastic difference in dynamics caused by the order of chemical reactions.

We characterize the weights w0, w1, w2 such that the weighted bilinear gradient inequality

holds for all functions , with a positive constant K independent of f1 and f2, for all possible values of q, p1 and p2 with 1 < q, p1, p2 < ∞.