Let E be an arbitrary set, a σ-algebra of subsets of

the Borel sets of F. We write A × B for the product of the sets A and B, and

for the product σ-algebra of and (i.e. the σ-algebra generated by the rectangles A × B with A ∈ and B ∈ ).

Let be a Dirichlet series. Then it is known that if is divergent, the abscissa of convergence σ1 is given by

and that if is divergent, the abscissa of absolute convergence σ2 is given by

A generalized Euler–Lagrange equation is presented. It provides a unified approach to boundary value problems in potential theory, diffusion, magnetostatics, and integral equations.

An alternative definition is proposed for the kernel used by Feynman. This definition involves a functional integration in a q, , p space, treating these variables as independent. The equivalence of this definition to the Feynman one and to the one using the variables q, p is exhibited.

An exact solution in terms of analytic functions is given for the Stokes stream function and forces acting on two spheres in contact when the spheres move uniformly with the same velocity along their line of centres. For the case of equal sized spheres, the values of the forces agree with the Faxén limit of the Stimson–Jeffery forces for separated spheres when the minimum clearance between the spheres tends to zero. Numerical values of the forces for arbitrary sized spheres are tabulated and compared with corresponding values when the spheres are separated over a range of values of the minimum clearance. Comparison of the theoretical results with those obtained experimentally for the case of equal sized spheres is also given.

In this paper we use a method due to Williams(1) to discuss the scattering of surface waves of small amplitude on water of infinite depth by a fixed vertical plane barrier extending indefinitely downwards from a finite depth.

It is shown that a revision is needed of certain transformation equations of the Planck–Einstein formulae. In particular it will be shown that the formulae

must be replaced by

where T and Q are respectively the absolute temperature and heat of the system. Furthermore, it will be shown that both formulae for the energy

are correct, but they refer to different cases.

Complementary variational principles are derived for a class of electrostatic and magnetostatic problems using the pairs of adjoint operators (grad, – div) and (curl, curl). This theory unifies the principles of Dirichlet and Thomson in electrostatics and of Schrader in magnetostatics. The results are illustrated by deriving upper and lower bounds for the capacity of a surface, and it is shown how such bounds can be systematically improved by Ritz procedures.

An alternative to Fock's proof of the uniqueness of the electromagnetic energy momentum tensor is presented. The proof is four-dimensional and is applicable in the curved space-time of general relativity.

The stress distribution, subject to a constant pressure over the entire surface of a penny-shaped crack is discussed by Sneddon(4). Recently, Robertson (3) has considered the diffraction of a plane longitudinal wave by a penny-shaped crack on a semi-infinite elastic solid. In the present analysis, the propagation of longitudinal wave in an infinite isotropic elastic plate with a penny-shaped crack in the middle has been investigated. The plane longitudinal wave is moving in the positive direction of z-azis and is impinging on the surface of the penny-shaped crack. The dual integral equation technique of Noble(l) is utilized to solve the mixed boundary-value problem. The analysis closely follows the method used in the author's previous paper (2). The vertical displacement is analysed numerically.

The title problem is solved by a semi-inverse method involving plane wave expansions. Expressions are given for stress singularities near the crack edge and for the radiation patterns produced by the crack. The case of an elliptical crack in an isotropic medium expanding under shear is examined in detail. Finally, some generalizations are discussed. Solutions are outlined for when the centre of the crack is allowed to move and for a self-similar phase transformation problem, in which a phase change takes place in an expanding ellipsoidal region.

The multiple scattering of plane harmonic P and S waves in an infinite elastic solid by arbitrary configurations of obstacles is considered. Integral equations relating the far-field multiple scattering amplitudes to the corresponding single scattering functions are obtained and asymptotic solutions are found by an iterative procedure. The scattering of a plane harmonic P wave by two identical rigid spheres is investigated.

Consider a linear elastic solid occupying a bounded regular three-dimensional region B with smooth surface ∂B. The components of displacement ui referred to cartesian axes xi are then well known to satisfy the system of governing equations

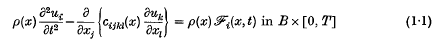
in which t denotes the time variable, x = (x1, x2, x3) denotes the position vector, ρ(x) is the non-homogeneous density, assumed positive,. 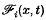i(x, t) are the Cartesian components of body force per unit mass, and cijkl(x) are the non-homogeneous elasticities, which apart from certain smoothness conditions stated later, are assumed to possess the symmetry

Throughout this paper, all suffixes range over the values 1, 2, 3 and the usual converition of summing over repeated indices is adopted. Except where it is in the interest of clarity we avoid explicit mention of the dependence of functions on their arguments.

The geometry of the Brillouin zone of antiferromagnetic NiO (Cc2/c) is studied. The corepresentations of the magnetic little group are deduced for the points and lines of symmetry. The magnon symmetries are investigated and the selection ruies for two magnon electric dipole and magnetic dipole absorption are deduced.