Analysis of the influence of an injected monochromatic wave on a turbulent spectrum shows that the evolution equation of the ensemble average distribution function is significantly different from the classical diffusion equation in velocity space. The average turbulent collision operator involves the usual spatial and temporal autocorrelation of the stochastic field, together with the correlation of this field with its spatial gradient, and the velocity derivatives are complemented by spatial derivatives

The general formalism for treating two-time fluctuations in magnetized plasma, developed in part 1 of this series, is applied to the case of anomalous cross-field transport in 2-D, strongly magnetized, thermal equilibrium systems. For 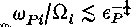(where εP is the plasma parameter), classical predictions for the ion shear viscosity and test particle diffusion coefficients are dominated by the anomalous contributions of low frequency, long wavelength hydrodynamic fluctuations (convective cells). The anomalous transport is discussed from the points of view of (a) kinetic theory; (b) the assumption of long-time local thermal equilibrium (Landau-Placzek method); and (c) a renormalized mode-coupling version of the generalized Langevin equation. The results of all these approaches are in agreement, and they predict that the transport coefficients scale with magnetic field B as 1/B for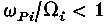, and as independent of B for

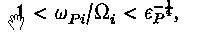
in good agreement with the computer simulations of Okuda & Dawson. The transport is weakly non-Markovian, the Green-Kubo integrands decay non-classically for long times as [t ln (t)]−½, and the test particle ‘;diffusion’ coefficient does not asymptotically approach a constant for t → ∞.

Resonant nonlinear interaction among three longitudinal waves propagating along any arbitrary angle to a uniform magnetic field in a plasma is investigated by a quantum-mechanical method. The coupled mode equations and coupling coefficients are derived.

Measurements of the m = 1 growing mode of a linear screw pinch, by external dipole probes, are compared with the recorded plasma motion on streak photographs. Good agreement is found up to a maximum amplitude which depends on plasma density and growth rate.

The oscillating-two-stream instability (OTSI) is shown to be a zero-frequency absolute instability of the backward-wave parametric type. The instability is shown to be distinct from the concurrent parametric-decay-instability (PDI), even for sub-critical pump frequencies very near the critical value. The analogous ‘purely-growing Brissllouin instability’ (POBI) is shown not to exist, in a collinear interaction, with a travelling-wave pump. In fact we conclude that no such backward-wave, zero frequency, absolute instability could occur in any case where the two interacting, frequency shifted waves are on the same mode of propagation as the travelling-wave pump. Finally, the possibility of a PGBI by means of a standing-wave pump, as suggested earlier by Lashmore-Davies, is confirmed for a collinear interaction, through the identification on the Brilbum diagram of a zero-frequency, back-wave parametric interaction resulting from the coupling of Stokes and anti-Stokes light waves by the standing-wave pumb light wave.

We investigate the electromotive force produced by plasma motions which are excited by an assigned body force. Two specific enquiries are made: (i) Can the Hall term create helicity in a plasma which is isotropically forced? (ii) What is the general form of the turbulent electromotive force when magnetic shear is present in the system? It proves possible to answer (ii) for weak shear in the two cases of weak and strong magnetic field.

A general dispersion relation is derived for linear waves in a non-uniform, magnetized plasma using the polarized co-ordinate system. An equilibrium distribution function with general gradients in density and temperature (and differing parallel and perpendicular temperatures) is proposed using polarized tensors. A compact conductivity tensor is derived in terms of tensor quantities, including certain tensor moment integrals whose elements may be evaluated separately from a given problem. This is of importance in computational applications. The derivation is under the restrictions (a) small gradients, (b) the local approximation of Krall & Rosenbluth, and (c) β⊥ ≪ 1. Conditions for coupling of electrostatic and electro-magnetic modes are investigated.

Electromagnetic ray propagation is discussed for weakly nonlinear dispersive media. Specialization to periodic waves justifies the use of a self-excitation model and facilitates the construction of a complete system of ray equations. The solution describes the evolution of frequencies, propagation vectors and amplitudes along the ray path. The formalism may be extended to include the case where a velocity field exists. This is based on special relativity and the Minkowski model for the electrodynamics of moving media. It is assumed that the velocity field varies slowly in space and time. The results are relevant to propagation problems in weakly nonlinear plasmas and optical media.

The parametric resonances involving the coupling of an external harmonic electric field to the plasmadynamical (PD) modes are studied. Particular attention is devoted to the resonant triplets involving purely dissipative PD modes of zero frequency. It is shown that a new type of instability exists in this class of processes.

Weak nonlinear coupling between two polarized transverse waves in a weakly relativistic plasma is studied including the effect of dispersion. The frequency of the coupled waves is of the same order of magnitude as the electron plasma frequency. By using the multiple scale method it is shown that the slow modulation of the complex amplitudes is described by simultaneous nonlinear Schrödinger equations. Travelling wave solutions are then obtained for this system of equations by the analytical and the numerical methods. As the result of the wave-wave interaction, two envelope waves are, in general, composed of dispersive shock waves or non-periodic nonlinear wave-trains, while the usual solitary waves or periodic nonlinear wave-trains can exist as a special case. case. The results of analysis can readily be applied to other coupled waves with different polarizations in a nonlinear dispersive medium.