We study the relationship between free curves and periodic points for torus homeomorphisms in the homotopy class of the identity. By free curve we mean a homotopically non-trivial simple closed curve that is disjoint from its image. We prove that every rational point in the rotation set is realized by a periodic point provided that there is no free curve and the rotation set has empty interior. This gives a topological version of a theorem of Franks. Using this result, and inspired by a theorem of Guillou, we prove a version of the Poincaré–Birkhoff theorem for torus homeomorphisms: in the absence of free curves, either there is a fixed point or the rotation set has non-empty interior.

We introduce a special class of pairwise-independent self-joinings for a stationary process: those for which one coordinate is a continuous function of the two others. We investigate which properties on the process the existence of such a joining entails. In particular, we prove that if the process is aperiodic, then it has positive entropy. Our other results suggest that such pairwise independent, non-independent self-joinings exist only in very specific situations: essentially when the process is a subshift of finite type topologically conjugate to a full-shift. This provides an argument in favor of the conjecture that two-fold mixing implies three-fold-mixing.

One of the unfulfilled aims of the authors of the preceding paper [W. Parry and M. Pollicott. An analogue of Bauer’s theorem for closed orbits of skew products. Ergod. Th. & Dynam. Sys.28 (2008), 535–546] was to find a dynamical analogue of Artin reciprocity. In this addendum, we present one such version, suggested by work of Sunada.

Let f be a germ of a holomorphic diffeomorphism of with the origin O being a quasi-parabolic fixed point, i.e. the spectrum of dfO consists of 1 and e2iπθj with . We show that f is locally holomorphically conjugated to its linear part, if f is of some particular form and its eigenvalues satisfy certain arithmetic conditions. When the spectrum of dfO does not consist of any 1’s, this is the classical result of Siegel [C. L. Siegel. Iteration of analytic functions. Ann. of Math.43 (1942), 607–612] and Brjuno [A. D. Brjuno. Analytic form of differential equations. Trans. Moscow Math. Soc.25 (1971), 131–288; 26 (1972), 199–239].

Let 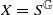where 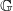is a countable group and S is a finite set. A cellular automaton (CA) is an endomorphism T:X→X (continuous, commuting with the action of 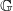). Shereshevsky [Expansiveness, entropy and polynomial growth for groups acting on subshifts by automorphisms. Indag. Math. (N.S.)4(2) (1993), 203–210] proved that for with d>1 no CA can be forward expansive, raising the following conjecture: for 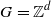, d>1, the topological entropy of any CA is either zero or infinite. Morris and Ward [Entropy bounds for endomorphisms commuting with K actions. Israel J. Math. 106 (1998), 1–11] proved this for linear CAs, leaving the original conjecture open. We show that this conjecture is false, proving that for any d there exists a d-dimensional CA with finite, non-zero topological entropy. We also discuss a measure-theoretic counterpart of this question for measure-preserving CAs.

In this paper we show that the quotient Aubry set, associated to a sufficiently smooth mechanical or symmetrical Lagrangian, is totally disconnected (i.e. every connected component consists of a single point). This result is optimal, in the sense of the regularity of the Lagrangian, as Mather’s counterexamples (J. N. Mather. Examples of Aubry sets. Ergod. Th. & Dynam. Sys.24(5) (2004), 1667–1723) show. Moreover, we discuss the relation between this problem and a Morse–Sard-type property for (the difference of) critical subsolutions of Hamilton–Jacobi equations.

We investigate the relationship between Poincaré recurrence and topological entropy of a dynamical system (X,f). For , let D(α,β) be the set of x with lower and upper recurrence rates α and β, respectively. Under the assumptions that the system is not minimal and that the map f is positively expansive and satisfies the specification condition, we show that for any open subset , has the full topological entropy of X. This extends a result of Feng and Wu [The Hausdorff dimension of recurrence sets in symbolic spaces. Nonlinearity14 (2001), 81–85] for symbolic spaces.

We consider suspension semi-flows of angle-multiplying maps on the circle for Cr ceiling functions with r≥3. Under a Crgeneric condition on the ceiling function, we show that there exists a Hilbert space (anisotropic Sobolev space) contained in the L2 space such that the Perron–Frobenius operator for the time-t-map acts naturally on it and that the essential spectral radius of that action is bounded by the square root of the inverse of the minimum expansion rate. This leads to a precise description of decay of correlations. Furthermore, the Perron–Frobenius operator for the time-t-map is quasi-compact for a Cr open and dense set of ceiling functions.

Let p be a hyperbolic periodic saddle of a diffeomorphism f on a closed manifold M, and let Cf(p) be the chain component of f containing p. In this paper, we show that if Cf(p) is C1-stably shadowable, then (i) Cf(p) is the homoclinic class of p and admits a dominated splitting (where the dimension of E is equal to that of the stable eigenspace of p); (ii) the Cf(p)-germ of f is expansive if and only if Cf(p) is hyperbolic; and (iii) when M is a surface, Cf(p) is locally maximal if and only if Cf (p) is hyperbolic.

We extend the renormalization group techniques that were developed originally for Hamiltonian flows to more general vector fields on 𝕋d×ℝℓ. Each Diophantine vector ω∈ℝd determines an analytic manifold 𝒲 of infinitely renormalizable vector fields, and each vector field on 𝒲 is shown to have an elliptic invariant d-torus with frequencies ω1,ω2,…,ωd. Analogous manifolds for particular classes of vector fields (Hamiltonian, divergence-free, symmetric, reversible) are obtained simply by restricting 𝒲 to the corresponding subspace. We also discuss non-degeneracy conditions, and the resulting reduction in the number of parameters needed in parametrized families to guarantee the existence of invariant tori.

We consider singular perturbation of a mixing subshift of finite type by means of thermodynamic formalism. In our formulation, the perturbed systems are described by a family of potentials {Φ(α,⋅)} with large parameter α on a fixed subshift of finite type, and the original (unperturbed) system is characterized as the system at infinity obtained by collapsing the perturbed system upon taking . We apply our formulation to the collapse of cookie-cutter systems and dispersing open billiards.

In this paper we study the liftability property for piecewise continuous maps of compact metric spaces, which admit inducing schemes in the sense of Pesin and Senti [Y. Pesin and S. Senti. Thermodynamical formalism associated with inducing schemes for one-dimensional maps. Mosc. Math. J.5(3) (2005), 669–678; Y. Pesin and S. Senti. Equilibrium measures for maps with inducing schemes. Preprint, 2007]. We show that under some natural assumptions on the inducing schemes—which hold for many known examples—any invariant ergodic Borel probability measure of sufficiently large entropy can be lifted to the tower associated with the inducing scheme. The argument uses the construction of connected Markov extensions due to Buzzi [J. Buzzi. Markov extensions for multi-dimensional dynamical systems. Israel J. Math.112 (1999), 357–380], his results on the liftability of measures of large entropy, and a generalization of some results by Bruin [H. Bruin. Induced maps, Markov extensions and invariant measures in one-dimensional dynamics. Comm. Math. Phys.168(3) (1995), 571–580] on relations between inducing schemes and Markov extensions. We apply our results to study the liftability problem for one-dimensional cusp maps (in particular, unimodal and multi-modal maps) and for some multi-dimensional maps.

In this paper, we exhibit, for any sparse-enough increasing sequence {pn} of integers, totally minimal, totally uniquely ergodic, and topologically mixing systems (X,T) and (X′,T′) and f∈C(X) for which the averages fail to converge on a residual set in X, and where there exists x′∈X′ with .

We introduce a class of vector fields on n-manifolds containing the hyperbolic systems, the singular-hyperbolic systems on 3-manifolds, the multidimensional Lorenz attractors and the robust transitive singular sets in Li et al [Robust transitive singular sets via approach of an extended linear Poincaré flow. Discrete Contin. Dyn. Syst.13(2) (2005), 239–269]. We prove that the closed orbits of a system in such a class are hyperbolic in a persistent way, a property which is false for higher-dimensional singular-hyperbolic systems. We also prove that the singularities in the robust transitive sets in Li et al are similar to those in the multidimensional Lorenz attractor. Our results will give a partial negative answer to Problem 9.26 in Bonatti et al [Dynamics Beyond Uniform Hyperbolicity. A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102. Mathematical Physics, III). Springer, Berlin, 2005].

Let U be the vector space of uniformly continuous real-valued functions on the real line and let U0 denote the subspace of U consisting of all bounded uniformly continuous functions. If X is a compact differentiable manifold and we are given a flow on X, then we associate with the flow a function F:X→H1(X,U/U0) that is invariant under the flow. We give examples for which the flow on X is ergodic but there is no λ∈H1(X,U/U0) such that F(p)=λ for almost all points p.

Suppose ℛ is a finite commutative ring of prime characteristic, 𝒜 is a finite ℛ-module, 𝕄:=ℤD×ℕE, and Φ is an ℛ-linear cellular automaton on 𝒜𝕄. If μ is a Φ-invariant measure which is multiply σ-mixing in a certain way, then we show that μ must be the Haar measure on a coset of some submodule shift of 𝒜𝕄. Under certain conditions, this means that μ must be the uniform Bernoulli measure on 𝒜𝕄.

In this paper we study the dynamics on and of a two-dimensional Blaschke product. We prove that in the case when the Blaschke product is a diffeomorphism of with all periodic points hyperbolic then the dynamics is hyperbolic. If a two-dimensional Blaschke product diffeomorphism of is embedded in a two-dimensional family given by composition with translations of , then we show that there is a non-empty open set of parameter values for which the dynamics is Anosov or has an expanding attractor with a unique SRB measure.

We prove large deviation principles for ergodic averages of dynamical systems admitting Markov tower extensions with exponential return times. Our main technical result from which a number of limit theorems are derived is the analyticity of logarithmic moment generating functions. Among the classes of dynamical systems to which our results apply are piecewise hyperbolic diffeomorphisms, dispersing billiards including Lorentz gases, and strange attractors of rank one including Hénon-type attractors.

Given a Polish space X, a countable Borel equivalence relation E on X, and a Borel cocycle , we characterize the circumstances under which there is a suitably non-trivial σ-finite measure μ on X such that, for every Borel injection ϕ whose graph is contained in E, ρ(ϕ−1(x),x)=[d(ϕ*μ)/dμ](x) μ-almost everywhere.

Veech showed that if a translation surface has a stabilizer which is a lattice in SL(2,ℝ), then any direction for the corresponding constant slope flow is either completely periodic or uniquely ergodic. We show that the converse does not hold: there are translation surfaces that satisfy Veech’s dichotomy but for which the corresponding stabilizer subgroup is not a lattice. The construction relies on work of Hubert and Schmidt.