For a 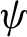 $\psi $
-mixing process
$\psi $
-mixing process
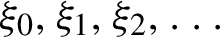 $\xi _0,\xi _1,\xi _2,\ldots $
we consider the number
$\xi _0,\xi _1,\xi _2,\ldots $
we consider the number
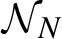 ${\mathcal N}_N$
of multiple returns
${\mathcal N}_N$
of multiple returns
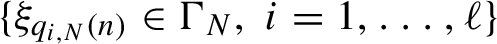 $\{\xi _{q_{i,N}(n)}\in {\Gamma }_N,\, i=1,\ldots ,\ell \}$
to a set
$\{\xi _{q_{i,N}(n)}\in {\Gamma }_N,\, i=1,\ldots ,\ell \}$
to a set
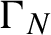 ${\Gamma }_N$
for n until either a fixed number N or until the moment
${\Gamma }_N$
for n until either a fixed number N or until the moment
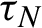 $\tau _N$
when another multiple return
$\tau _N$
when another multiple return
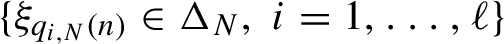 $\{\xi _{q_{i,N}(n)}\in {\Delta }_N,\, i=1,\ldots ,\ell \}$
, takes place for the first time where
$\{\xi _{q_{i,N}(n)}\in {\Delta }_N,\, i=1,\ldots ,\ell \}$
, takes place for the first time where
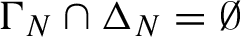 ${\Gamma }_N\cap {\Delta }_N=\emptyset $
and
${\Gamma }_N\cap {\Delta }_N=\emptyset $
and
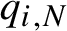 $q_{i,N}$
,
$q_{i,N}$
,
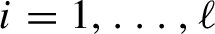 $i=1,\ldots ,\ell $
are certain functions of n taking on non-negative integer values when n runs from 0 to N. The dependence of
$i=1,\ldots ,\ell $
are certain functions of n taking on non-negative integer values when n runs from 0 to N. The dependence of
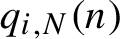 $q_{i,N}(n)$
on both n and N is the main novelty of the paper. Under some restrictions on the functions
$q_{i,N}(n)$
on both n and N is the main novelty of the paper. Under some restrictions on the functions
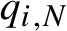 $q_{i,N}$
we obtain Poisson distributions limits of
$q_{i,N}$
we obtain Poisson distributions limits of
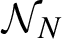 ${\mathcal N}_N$
when counting is until N as
${\mathcal N}_N$
when counting is until N as
 $N\to \infty $
and geometric distributions limits when counting is until
$N\to \infty $
and geometric distributions limits when counting is until
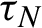 $\tau _N$
as
$\tau _N$
as
 $N\to \infty $
. We obtain also similar results in the dynamical systems setup considering a
$N\to \infty $
. We obtain also similar results in the dynamical systems setup considering a
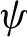 $\psi $
-mixing shift T on a sequence space
$\psi $
-mixing shift T on a sequence space
 ${\Omega }$
and studying the number of multiple returns
${\Omega }$
and studying the number of multiple returns
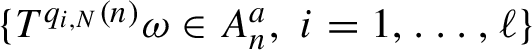 $\{ T^{q_{i,N}(n)}{\omega }\in A^a_n,\, i=1,\ldots ,\ell \}$
until the first occurrence of another multiple return
$\{ T^{q_{i,N}(n)}{\omega }\in A^a_n,\, i=1,\ldots ,\ell \}$
until the first occurrence of another multiple return
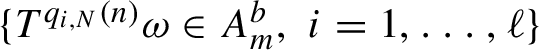 $\{ T^{q_{i,N}(n)}{\omega }\in A^b_m,\, i=1,\ldots ,\ell \}$
where
$\{ T^{q_{i,N}(n)}{\omega }\in A^b_m,\, i=1,\ldots ,\ell \}$
where
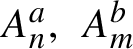 $A^a_n,\, A_m^b$
are cylinder sets of length n and m constructed by sequences
$A^a_n,\, A_m^b$
are cylinder sets of length n and m constructed by sequences
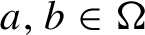 $a,b\in {\Omega }$
, respectively, and chosen so that their probabilities have the same order.
$a,b\in {\Omega }$
, respectively, and chosen so that their probabilities have the same order.
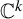 $\mathbb {C}^k$
$\mathbb {C}^k$
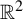 $\mathbb {R}^2$
generated by a generalized substitution
$\mathbb {R}^2$
generated by a generalized substitution