For a graph H and an integer r ≥ 2, the induced r-size-Ramsey number of H is defined to be the smallest integer m for which there exists a graph G with m edges with the following property: however one colours the edges of G with r colours, there always exists a monochromatic induced subgraph H′ of G that is isomorphic to H. This is a concept closely related to the classical r-size-Ramsey number of Erdős, Faudree, Rousseau and Schelp, and to the r-induced Ramsey number, a natural notion that appears in problems and conjectures due to, among others, Graham and Rödl, and Trotter. Here, we prove a result that implies that the induced r-size-Ramsey number of the cycle Cℓ is at most crℓ for some constant cr that depends only upon r. Thus we settle a conjecture of Graham and Rödl, which states that the above holds for the path Pℓ of order ℓ and also generalise in part a result of Bollobás, Burr and Reimer that implies that the r-size Ramsey number of the cycle Cℓ is linear in ℓ Our method of proof is heavily based on techniques from the theory of random graphs and on a variant of the powerful regularity lemma of Szemerédi.
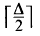 Linear Forests
Linear Forests