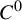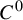Let M be a compact smooth manifold without boundary. Based on results by Good and Meddaugh [Invent. Math. 220 (2020), 715–736], we prove that a strong distributional chaos is
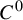 $C^0$
-generic in the space of continuous self-maps (respectively, homeomorphisms) of M. The results contain answers to questions by Li, Li and Tu [Chaos 26 (2016), 093103] and Moothathu [Topology Appl. 158 (2011), 2232–2239] in the zero-dimensional case. A related counter-example on the chain components under shadowing is also given.
$C^0$
-generic in the space of continuous self-maps (respectively, homeomorphisms) of M. The results contain answers to questions by Li, Li and Tu [Chaos 26 (2016), 093103] and Moothathu [Topology Appl. 158 (2011), 2232–2239] in the zero-dimensional case. A related counter-example on the chain components under shadowing is also given.
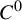 $C^0$
-genericity of distributional chaos
$C^0$
-genericity of distributional chaos