It is well known that spectral methods (tau, Galerkin, collocation) have a condition number of O(N4) where N is the number of retained modes of polynomial approximations. This paper presents some efficient spectral algorithms, which have a condition number of O(N2), based on the ultraspherical-Galerkin methods for the integrated forms of second-order elliptic equations in one and two space variables. The key to the efficiency of these algorithms is to construct appropriate base functions, which lead to systems with specially structured matrices that can be efficiently inverted. The complexities of the algorithms are a small multiple of Nd+1 operations for a d-dimensional domain with (N – 1)d unknowns, while the convergence rates of the algorithms are exponentials with smooth solutions.

We define the higher order Riesz transforms and the Littlewood-Paley $g$-function associated to the differential operator 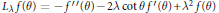${{L}_{\lambda }}f(\theta )\,=\,-{f}''(\theta )-2\lambda \cot \theta {f}'(\theta )+{{\lambda }^{2}}f(\theta )$. We prove that these operators are Calderón–Zygmund operators in the homogeneous type space 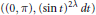$((0,\,\pi ),\,{{(\sin t)}^{2\lambda }}dt)$. Consequently, 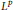${{L}^{p}}$ weighted, 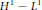${{H}^{1}}\,-\,{{L}^{1}}$ and 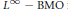${{L}^{\infty }}\,-\,BMO$ inequalities are obtained.