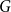We study the problem of finding pairwise vertex-disjoint triangles in the randomly perturbed graph model, which is the union of any $n$ -vertex graph $G$ satisfying a given minimum degree condition and the binomial random graph 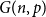$G(n,p)$ . We prove that asymptotically almost surely 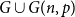$G \cup G(n,p)$ contains at least 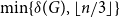$\min \{\delta (G), \lfloor n/3 \rfloor \}$ pairwise vertex-disjoint triangles, provided 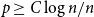$p \ge C \log n/n$ , where 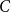$C$ is a large enough constant. This is a perturbed version of an old result of Dirac.

Our result is asymptotically optimal and answers a question of Han, Morris, and Treglown [RSA, 2021, no. 3, 480–516] in a strong form. We also prove a stability version of our result, which in the case of pairwise vertex-disjoint triangles extends a result of Han, Morris, and Treglown [RSA, 2021, no. 3, 480–516]. Together with a result of Balogh, Treglown, and Wagner [CPC, 2019, no. 2, 159–176], this fully resolves the existence of triangle factors in randomly perturbed graphs.

We believe that the methods introduced in this paper are useful for a variety of related problems: we discuss possible generalisations to clique factors, cycle factors, and 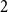$2$ -universality.