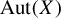Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

synchronized shifts

Ergodic Theory and Dynamical Systems (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

Glider automata on all transitive sofic shifts
Part of
- Topological dynamics
JOHAN KOPRA
Journal:

Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022

Published online by Cambridge University Press:

30 September 2021, pp. 3716-3744

Print publication:

December 2022
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
For any infinite transitive sofic shift X we construct a reversible cellular automaton (that is, an automorphism of the shift X) which breaks any given finite point of the subshift into a finite collection of gliders traveling into opposing directions. This shows in addition that every infinite transitive sofic shift has a reversible cellular automaton which is sensitive with respect to all directions. As another application we prove a finitary version of Ryan’s theorem: the automorphism group 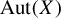$\operatorname {\mathrm {Aut}}(X)$ contains a two-element subset whose centralizer consists only of shift maps. We also show that in the class of S-gap shifts these results do not extend beyond the sofic case.