We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Z.-W. Sun [‘Refining Lagrange’s four-square theorem’, J. Number Theory175 (2017), 169–190] conjectured that
every positive integer n can be written as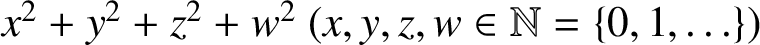 
$ x^2+y^2+z^2+w^2\ (x,y,z,w\in \mathbb {N}=\{0,1,\ldots \})$
with
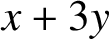$x+3y$
a square and also as
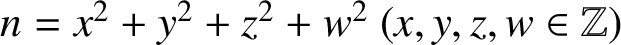$n=x^2+y^2+z^2+w^2\ (x,y,z,w \in \mathbb {Z})$
with
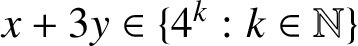$x+3y\in \{4^k:k\in \mathbb {N}\}$
. In this paper, we confirm these conjectures via the arithmetic theory of ternary quadratic forms.
