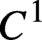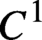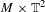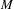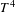We show that a sectional-hyperbolic attracting set for a Hölder- $C^{1}$ vector field admits finitely many physical/SRB measures whose ergodic basins cover Lebesgue almost all points of the basin of topological attraction. In addition, these physical measures depend continuously on the flow in the $C^{1}$ topology, that is, sectional-hyperbolic attracting sets are statistically stable. To prove these results we show that each central-unstable disk in a neighborhood of this class of attracting sets is eventually expanded to contain a ball whose inner radius is uniformly bounded away from zero.

We consider skew products on 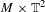$M\times \mathbb{T}^{2}$, where 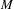$M$ is the two-sphere or the two-torus, which are partially hyperbolic and semi-conjugate to an Axiom A diffeomorphism. This class of dynamics includes the open sets of $\unicode[STIX]{x1D6FA}$-non-stable systems introduced by Abraham and Smale [Non-genericity of Ł-stability. Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV (Berkeley 1968)). American Mathematical Society, Providence, RI, 1970, pp. 5–8.] and Shub [Topological Transitive Diffeomorphisms in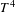$T^{4}$ (Lecture Notes in Mathematics, 206). Springer, Berlin, 1971, pp. 39–40]. We present sufficient conditions, both on the skew products and the potentials, for the existence and uniqueness of equilibrium states, and discuss their statistical stability.

We contribute to the thermodynamic formalism of partially hyperbolic attractors for local diffeomorphisms admitting an invariant stable bundle and a positively invariant cone field with non-uniform cone expansion at a positive Lebesgue measure set of points. These include the case of attractors for Axiom A endomorphisms and partially hyperbolic endomorphisms derived from Anosov. We prove these attractors have finitely many SRB measures, that these are hyperbolic, and that the SRB measure is unique provided the dynamics is transitive. Moreover, we show that the SRB measures are statistically stable (in the weak$^{\ast }$ topology) and that their entropy varies continuously with respect to the local diffeomorphism.