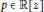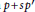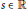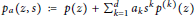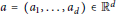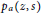We prove that projective spaces of Lorentzian and real stable polynomials are homeomorphic to Euclidean balls. This solves a conjecture of June Huh and the author. The proof utilises and refines a connection between the symmetric exclusion process in interacting particle systems and the geometry of polynomials.

We consider homogeneous multiaffine polynomials whose coefficients are the Plücker coordinates of a point $V$ of the Grassmannian. We show that such a polynomial is stable (with respect to the upper half plane) if and only if $V$ is in the totally nonnegative part of the Grassmannian. To prove this, we consider an action of matrices on multiaffine polynomials. We show that a matrix $A$ preserves stability of polynomials if and only if $A$ is totally nonnegative. The proofs are applications of classical theory of totally nonnegative matrices, and the generalized Pólya-Schur theory of Borcea and Brändén.

Nuij's theorem states that if a polynomial 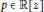$p\in \mathbb{R}[z]$ is hyperbolic (i.e., has only real roots), then 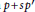$p+s{{p}^{'}}$ is also hyperbolic for any 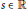$s\in \mathbb{R}$. We study other perturbations of hyperbolic polynomials of the form 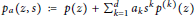${{p}_{a}}(z,s)\,\,:=\,\,\,p\,(z)+\,\sum\nolimits_{k=1}^{d}{{{a}_{k}}{{s}^{k}}{{p}^{(k)}}(z)}$. We give a full characterization of those 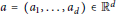$a=({{a}_{1}},...,{{a}_{d}})\,\in \,{{\mathbb{R}}^{d}}$ for which 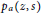${{p}_{a}}(z,s)$ is a pencil of hyperbolic polynomials. We also give a full characterization of those 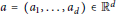$a=({{a}_{1}},...,{{a}_{d}})\,\in \,{{\mathbb{R}}^{d}}$ for which the associated families 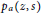$ $ admit universal determinantal representations. In fact, we show that all these sequences come fromspecial symmetric Toeplitz matrices.