The tower number 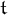 ${\mathfrak t}$ and the ultrafilter number
${\mathfrak t}$ and the ultrafilter number 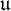 $\mathfrak {u}$ are cardinal characteristics from set theory. They are based on combinatorial properties of classes of subsets of
$\mathfrak {u}$ are cardinal characteristics from set theory. They are based on combinatorial properties of classes of subsets of 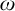 $\omega $ and the almost inclusion relation
$\omega $ and the almost inclusion relation 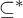 $\subseteq ^*$ between such subsets. We consider analogs of these cardinal characteristics in computability theory.
$\subseteq ^*$ between such subsets. We consider analogs of these cardinal characteristics in computability theory.
We say that a sequence 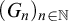 $(G_n)_{n \in {\mathbb N}}$ of computable sets is a tower if
$(G_n)_{n \in {\mathbb N}}$ of computable sets is a tower if 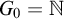 $G_0 = {\mathbb N}$,
$G_0 = {\mathbb N}$, 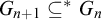 $G_{n+1} \subseteq ^* G_n$, and
$G_{n+1} \subseteq ^* G_n$, and 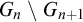 $G_n\smallsetminus G_{n+1}$ is infinite for each n. A tower is maximal if there is no infinite computable set contained in all
$G_n\smallsetminus G_{n+1}$ is infinite for each n. A tower is maximal if there is no infinite computable set contained in all 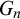 $G_n$. A tower
$G_n$. A tower 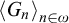 ${\left \langle {G_n}\right \rangle }_{n\in \omega }$ is an ultrafilter base if for each computable R, there is n such that
${\left \langle {G_n}\right \rangle }_{n\in \omega }$ is an ultrafilter base if for each computable R, there is n such that 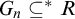 $G_n \subseteq ^* R$ or
$G_n \subseteq ^* R$ or 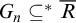 $G_n \subseteq ^* \overline R$; this property implies maximality of the tower. A sequence
$G_n \subseteq ^* \overline R$; this property implies maximality of the tower. A sequence 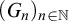 $(G_n)_{n \in {\mathbb N}}$ of sets can be encoded as the “columns” of a set
$(G_n)_{n \in {\mathbb N}}$ of sets can be encoded as the “columns” of a set 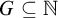 $G\subseteq \mathbb N$. Our analogs of
$G\subseteq \mathbb N$. Our analogs of 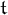 ${\mathfrak t}$ and
${\mathfrak t}$ and 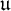 ${\mathfrak u}$ are the mass problems of sets encoding maximal towers, and of sets encoding towers that are ultrafilter bases, respectively. The relative position of a cardinal characteristic broadly corresponds to the relative computational complexity of the mass problem. We use Medvedev reducibility to formalize relative computational complexity, and thus to compare such mass problems to known ones.
${\mathfrak u}$ are the mass problems of sets encoding maximal towers, and of sets encoding towers that are ultrafilter bases, respectively. The relative position of a cardinal characteristic broadly corresponds to the relative computational complexity of the mass problem. We use Medvedev reducibility to formalize relative computational complexity, and thus to compare such mass problems to known ones.
We show that the mass problem of ultrafilter bases is equivalent to the mass problem of computing a function that dominates all computable functions, and hence, by Martin’s characterization, it captures highness. On the other hand, the mass problem for maximal towers is below the mass problem of computing a non-low set. We also show that some, but not all, noncomputable low sets compute maximal towers: Every noncomputable (low) c.e. set computes a maximal tower but no 1-generic 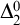 $\Delta ^0_2$-set does so.
$\Delta ^0_2$-set does so.
We finally consider the mass problems of maximal almost disjoint, and of maximal independent families. We show that they are Medvedev equivalent to maximal towers, and to ultrafilter bases, respectively.