We present recursions for the total number, Sn, of mutations in a sample of n individuals, when the underlying genealogical tree of the sample is modelled by a coalescent process with mutation rate r>0. The coalescent is allowed to have simultaneous multiple collisions of ancestral lineages, which corresponds to the existence of large families in the underlying population model. For the subclass of Λ-coalescent processes allowing for multiple collisions, such that the measure Λ(dx)/x is finite, we prove that Sn/(nr) converges in distribution to a limiting variable, S, characterized via an exponential integral of a certain subordinator. When the measure Λ(dx)/x2 is finite, the distribution of S coincides with the stationary distribution of an autoregressive process of order 1 and is uniquely determined via a stochastic fixed-point equation of the form 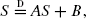 with specific independent random coefficients A and B. Examples are presented in which explicit representations for (the density of) S are available. We conjecture that Sn/E(Sn)→1 in probability if the measure Λ(dx)/x is infinite.
with specific independent random coefficients A and B. Examples are presented in which explicit representations for (the density of) S are available. We conjecture that Sn/E(Sn)→1 in probability if the measure Λ(dx)/x is infinite.

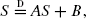 with specific independent random coefficients
with specific independent random coefficients 