We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Recently, Daws introduced a notion of co-representation of abelian Hopf–von Neumann algebras on general reflexive Banach spaces. In this note, we show that this notion cannot be extended beyond subhomogeneous Hopf–von Neumann algebras. The key is our observation that, for a von Neumann algebra 𝔐 and a reflexive operator space E, the normal spatial tensor product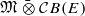 
is a Banach algebra if and only if 𝔐 is subhomogeneous or E is completely isomorphic to column Hilbert space.
