We consider the task completion time of a repairable server system in which a server experiences randomly occurring service interruptions during which the server works slowly. Every service-state change preempts the task that is being processed. The server may then resume the interrupted task, it may replace the task with a different one, or it may restart the same task from the beginning, under the new service-state. The total time that the server takes to complete a task of random size including interruptions is called completion time. We study the completion time of a task under the last two cases as a function of the task size distribution, the service interruption frequency/severity, and the repair frequency. We derive closed form expressions for the completion time distribution in Laplace domain under replace and restart recovery disciplines and present their asymptotic behavior. In general, the heavy tailed behavior of completion times arises due to the heavy tailedness of the task time. However, in the preempt-restart service discipline, even in the case that the server still serves during interruptions albeit at a slower rate, completion times may demonstrate power tail behavior for exponential tail task time distributions. Furthermore, we present an 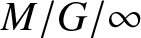$M/G/\infty$ queue with exponential service time and Markovian service interruptions. Our results reveal that the stationary first order moments, that is, expected system time and expected number in the system are insensitive to the way the service modulation affects the servers; system-wide modulation affecting every server simultaneously vs identical modulation affecting each server independently.

Consider a random environment in ${\mathbb Z}^d$ given by i.i.d. conductances.In this work, we obtain tail estimates for the fluctuations about themean for the following characteristics of the environment: the effective conductance between opposite faces of a cube, the diffusion matrices of periodized environmentsand the spectral gap of the random walk in a finite cube.

A basic issue in extreme value theory is the characterization of the asymptotic distribution of the maximum of a number of random variables as the number tends to infinity. We address this issue in several settings. For independent identically distributed random variables where the distribution is a mixture, we show that the convergence of their maxima is determined by one of the distributions in the mixture that has a dominant tail. We use this result to characterize the asymptotic distribution of maxima associated with mixtures of convolutions of Erlang distributions and of normal distributions. Normalizing constants and bounds on the rates of convergence are also established. The next result is that the distribution of the maxima of independent random variables with phase type distributions converges to the Gumbel extreme-value distribution. These results are applied to describe completion times for jobs consisting of the parallel-processing of tasks represented by Markovian PERT networks or task-graphs. In these contexts, which arise in manufacturing and computer systems, the job completion time is the maximum of the task times and the number of tasks is fairly large. We also consider maxima of dependent random variables for which distributions are selected by an ergodic random environment process that may depend on the variables. We show under certain conditions that their distributions may converge to one of the three classical extreme-value distributions. This applies to parallel-processing where the subtasks are selected by a Markov chain.

We derive a variety of estimates for the survival probability of a branching process in a random environment. There are three cases of interest, the critical, weakly and strongly subcritical. The large deviation result, first obtained by Dekking for the class of finite state space i.i.d. environments, is shown to hold in more general environments. We also obtain some finer convergence results.

Let {Zn} be a Galton-Watson process with i.i.d. random environments. This paper is concerned with estimation of π= E log Mn, where Mn is the. conditional expected number of offspring per nth generation individual, given the environments, when this quantity is positive. We show that, given non-extinction, {n-1 log Zn} is asymptotically the most efficient estimator of πamongst a broad class of those that are linear combinations of {log Zi: 1 ≦ j ≦ n}·

A model of the effects of random variations in environment upon reproductive fitness of sexual and asexual members of a population is analyzed, using individual selection arguments. Conditions are found under which sexuality does result in a net selective advantage, with the conditions per locus becoming markedly less severe as the number of loci considered increases.

The general framework of a Markov chain in a random environment is presented and the problem of determining extinction probabilities is discussed. An efficient method for determining absorption probabilities and criteria for certain absorption are presented in the case that the environmental process is a two-state Markov chain. These results are then applied to birth and death, queueing and branching chains in random environments.

Let w1, w12 and w2 be the fitnesses of genotypes A1A1, A1A2 and A2A2 in an infinite diploid population, and let pn be the A1, gene frequency in the nth generation. If fitness varies independently from generation to generation, then pn is a Markov process with a continuum of states. If E[In(wi/w12)] < 0 for i = 1, 2, then there is a unique stationary probability, and the distribution of pn converges to it as n → ∞.

R-positivity theory for Markov chains is used to obtain results for random environment branching processes whose environment random variables are independent and identically distributed and whose environmental extinction probabilities are equal. For certain processes whose eventual extinction is almost sure, it is shown that the distribution of population size conditioned by non-extinction at time n tends to a left eigenvector of the transition matrix. Limiting values of other conditional probabilities are given in terms of this left eigenvector and it is shown that the probability of non-extinction at time n approaches zero geometrically as n approaches ∞. Analogous results are obtained for processes whose extinction is not almost sure.

A conditional Poisson process (often called a double stochastic Poisson process) is characterized as a random time transformation of a Poisson process with unit intensity. This characterization is used to exhibit the jump times and sizes of these processes, and to study their limiting behavior. A conditional Poisson process, whose intensity is a function of a Markov process, is discussed. Results similar to those presented can be obtained for any process with conditional stationary independent increments.