We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We present a Markov chain example where non-reversibility and an added edge jointly improve mixing time. When a random edge is added to a cycle of n vertices and a Markov chain with a drift is introduced, we get a mixing time of
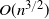$O(n^{3/2})$
with probability bounded away from 0. If only one of the two modifications were performed, the mixing time would stay
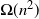$\Omega(n^2)$
.
