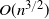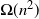Analysis of a non-reversible Markov chain speedup by a single edge

Abstract

We present a Markov chain example where non-reversibility and an added edge jointly improve mixing time. When a random edge is added to a cycle of n vertices and a Markov chain with a drift is introduced, we get a mixing time of $O(n^{3/2})$ with probability bounded away from 0. If only one of the two modifications were performed, the mixing time would stay $\Omega(n^2)$ .

1. Introduction

The fundamentals of Markov chain theory are well established, but it is still in constant development with various motivations from applications and inspiring sparks from novel discoveries [1, 13]. Understanding mixing gives an insight on the macroscopic behavior of the dynamics of the chain; moreover, it is also a crucial factor determining the efficiency of applications built using the chain. The Markov chain Monte Carlo approach is a popular scheme to translate mixing of Markov chains into powerful methods for sampling or numerical integration [6].

Simple examples realizing new phenomena, either expected or surprising, help the community to get a deeper understanding of what is possible, and how. The aim of the current paper is to present and discuss such an example.

The starting point is the cycle with n vertices, see Figure 1(a), where we consider the class of Markov chains whose stationary distribution is uniform. For reversible Markov chains (meaning that the stationary frequency of transition along every edge is the same in the two directions), standard results [5, 13] show that the mixing time is $\Omega(n^2)$ .

Figure 1. Cycle graph with either (a) no extra edges, (b) all parallel edges between opposing vertices, or (c) a single random extra edge.

Relaxing the reversibility condition does not help in this simple case. An important observation is that we only get a single extra degree of freedom, a possible drift: we may increase all clockwise and decrease all counter-clockwise transition probabilities by the same amount departing from a reversible transition structure. It is a surprisingly non-trivial result [9] that the mixing time is still $\Omega(n^2)$ .

Still striving for faster mixing, we may analyze a graph with additional edges. It was a key revelation of [7] that when edges connecting opposing vertices are available, as in Figure 1(b), and a strong drift is used, the mixing time drops to O(n) (this is a slight reinterpretation of their context).

What happens if we use fewer extra edges? In this paper we want to understand the other extreme, when the number of added edges is one. We choose a single extra edge randomly, see Figure 1(c). For any reversible chain, the mixing time is again $\Omega(n^2)$ as there is still a path of length of order n without any other edge.

However, if again combined with a drift along the cycle, we may get a considerable speedup, with the mixing time decreasing to $O(n^{3/2})$ with probability bounded away from 0.

Related models in the literature have appeared demonstrating that this $n^{3/2}$ order may emerge. [2] considered a card shuffling model where either the bottom card or one from a fixed position is put on top. Following a single card in the shuffle, they show $n^{3/2}$ for asymptotically all choices of the fixed position, but computing only the inverse spectral gap, thus capturing only asymptotic but not finite-time behavior.

A model closer to the current investigation is considered in [4], where two equal-size cycles are glued together at a vertex, both with a biased walk on them, and the amount of bias is modified for one of the cycles. This may result in a Markov chain with mixing time of $\Omega(n^{3/2})$ . Their theorem is stated for one specific value of the modification, but the proof is valid for any badly approximable amount in the Diophantine sense, which provides a range of full Hausdorff dimension but zero Lebesgue measure [11, 12].

For the current model, the nature of our results, Theorems 1 and 2, are conceptually in between the above. We cannot capture asymptotically almost sure upper bounds at the moment, but have a positive lower bound on the proportion of favorable cases, and for those the order of the mixing time is properly determined.

Let us now proceed to the necessary formal definitions and precise statements.

2. Preliminaries and main results

Formally the Markov chains of interest X(t) can be built as follows.

Definition 1. Consider a cycle graph of n vertices on $V=\{1,2,\ldots,n\}$ . To add a new edge, by symmetry, we assume without loss of generality that one endpoint is n. Choose a uniform random integer k from $[2,n-2]$ , and add the edge (k, n). We will name the vertices k, n hubs. For convenience, on the arc $1,2,\ldots,k$ we introduce the notation $a_1,a_2,\ldots, a_k$ for the vertices and name the arc A, while on the arc $k+1,k+2,\ldots,n$ we use $b_1,b_2,\ldots,b_{n-k}$ and B. Using the convention $P(X(t+1) = j \mid X(t) = i) \;=\!:\; P(i,j)$ for the transition probabilities, we set

\begin{align*} P(a_i,a_{i+1}) &= P(b_j,b_{j+1}) = \tfrac{1}{2} \quad \mathrm{for\ all}\ 1 \le i \le k - 1,\ 1 \le j \le n - k - 1, \\[5pt] P(a_k,b_1) & = P(b_{n-k},a_1) = \tfrac{1}{2}, \\[5pt] P(a_i,a_i) & = P(b_j,b_j) = \tfrac{1}{2} \quad \mathrm{for\ all}\ 1 \le i \le k - 1,\ 1 \le j \le n - k - 1, \\[5pt] P(a_k,a_k) & = P(a_k,b_{n-k}) = P(b_{n-k},a_k) = P(b_{n-k},b_{n-k}) = \tfrac{1}{4}. \end{align*}

Set all other transition probabilities to 0.

Note that we exclude the possible values 1, $n-1$ , and n for k, not only for the intuitive reason of getting a real additional edge with (k, n), but also to avoid conflicting transition probability definitions.

It is easy to verify that this transition kernel is doubly stochastic, and therefore is a valid transition kernel with the uniform distribution as the stationary distribution (aperiodicity, irreducibility ensures uniqueness). For initialization, set X(0) deterministically to any vertex of preference.

For any random variable Y, let ${\mathcal{L}}(Y)$ denote its distribution. We are going to compare probability distributions with their total variation distance. For any probability distributions $\mu,\sigma$ , this is defined as

\begin{align*} \|\mu-\sigma\|_{\rm TV} \;:\!=\; \sup_{S\subseteq V}|\mu(S)-\sigma(S)| = \frac{1}{2}\sum_{x\in V}|\mu(x)-\sigma(x)|.\end{align*}

Keeping in mind that currently the stationary distribution is uniform, which we denote by $\frac{{\textbf{1}}}{n}$ , we define the maximal distance and the mixing time as

(1) \begin{align} d_X(t) &\;:\!=\;\sup_{X(0)\in V}\bigg\|{\mathcal{L}}(X(t))-\frac{{\textbf{1}}}{n}\bigg\|_{\rm TV}, \end{align}

(2) \begin{align} t_{\rm mix}(X,{\varepsilon})&\;:\!=\;\min\{t\colon d_X(t) \le {\varepsilon}\}. \end{align}

We will omit X when it is clear from the context. We now have all the ingredients to state our main results.

Theorem 1. There exist constants $\gamma, \gamma'>0$ such that, for any $\frac{1}{2} > {\varepsilon} > 0$ , the following holds. For the (randomized) Markov chain of Definition 1, for n large enough, with probability at least $\gamma$ we have $t_{\rm mix}({\varepsilon}) \le \gamma' n^{3/2} \log({1}/{{\varepsilon}})$ .

Theorem 2. There exist constants $\gamma^*, {\varepsilon}^*>0$ such that, for the (randomized) Markov chain of Definition 1, for n large enough we (deterministically) have $t_{\rm mix}({\varepsilon}^*) \ge \gamma^* n^{3/2}$ .

During the statements and proofs various non-explicit global constants will appear, denoted by $\gamma_i$ . To ensure there is no circular dependence, as a general rule we index them in order so that the value of $\gamma_i$ may be chosen and fixed once all $\gamma_{i'}$ are determined for $i'<i$ . The final constants $\gamma$ , $\gamma'$ , $\gamma^*$ , and ${\varepsilon}^*$ of Theorems 1 and 2 might depend on all of them. We will carry through a time scaling constant $\rho$ , which we can take to be 1 for most of the paper but we will need this extra flexibility for the lower bound. We use various $\beta_j$ during the proofs, but only for the scope of the proof; they might be reused later. Currently our Markov chain is based on the cycle, so we will use the metric on it, therefore $|i-j|$ will often be used as a simplification for $\min(|i-j|, n-|i-j|)$ when appropriate.

To provide an initial intuition for the order of the mixing time, note that approximately $n^{3/2}$ random steps on arcs of length approximately n correspond to approximately $n^{1/2}$ random choices of arcs. For these random choices, they typically concentrate near approximately $n^{1/4}$ possibilities when added up. On the other hand, local steps themselves by the loop probabilities provide an overall diffusion of size approximately $n^{3/4}$ . Thus, the jumps and local diffusions together with approximately $n^{1/4+3/4}$ coverage are sufficient for overall mixing. These heuristics will be described formally later, together with the corresponding calculations.

The rest of the paper is organized as follows. First, we analyze the path taken after a certain number of moves and represent it on a square grid. We give estimates on reaching certain points of interest on this grid; this is worked out in Section 3. Then, we investigate the connection of the grid to our original graph in Section 4. In Section 5 we switch from possible tracks to the actual Markov chain and examine the diffusive randomness that appears. In Section 6 we join the elements to get a complete proof of Theorem 1. We adjust this viewpoint to obtain the lower bound of Theorem 2 in Section 7. Finally, we conclude in Section 8.

3. Grid representation of the tracks

As a first step, we want to understand the track of the Markov chain traversed without the time taken to walk through it. That is, we disregard loop steps, and we also disregard (possibly repeated) hopping between hubs; in this sense we will often treat the two hubs together. This means that for our purposes the track of the Markov chain is composed of traversing an arc, then choosing the next when reaching the pair of hubs, then traversing another one, and so on.

In order to represent and record this, consider the non-negative quadrant of the square integer lattice together with a direction, i.e. ${\mathbb{Z}}_+^2\times H$ , where $H = \{A,B\}$ . A position (x, y, h) represents that the Markov chain has taken the A arc x times, the B arc y times, and has arrived at the position on a horizontal (A) or vertical (B) segment. A track on the cycle is then partially represented by a walk on this grid with non-decreasing coordinates; we at least see the $A/B$ statistics developing. We may also translate intermediate points of the grid lines of the non-negative quadrant to represent them as being within a certain arc (after completely traversing some previously). Note that when traveling through an arc, say A, we already know that the only possibility in a few more steps is to have an arc A completely passed. Therefore, the meaningful interpretation for such points on the grid is to interpolate on the x coordinate and to set $h=A$ throughout once moving on the arc. The space in which these tracks move is therefore contained in

\begin{align*} R_*=\{(x,y,h)\in {\mathbb{R}}_+^2\times H \mid (x\in{\mathbb{Z}}_+,h=B) \textrm{ or } (y\in{\mathbb{Z}}_+,h=A)\}.\end{align*}

Note that at grid points of ${\mathbb{Z}}_+^2$ the arcs would overlap, representing both $a_k$ and $b_{n-k}$ ; this is the reason for the extra property of direction. Now all tracks can be represented as moving along $R_*$ with non-decreasing coordinates. At the initial point there are no traversed arcs yet, so X(0) corresponds to a point $(\!-\!\lambda, 0, A)$ or $(0,-\lambda, B)$ for some $\lambda\in [0,1)$ . This structure can be seen in Figure 2.

Figure 2. Illustration of ${\mathbb{Z}}_+^2\times H$ . Points of the form $(\cdot,\cdot,A)$ are represented by gray dots while $(\cdot,\cdot,B)$ points are represented by black dots. The extension to $R_*$ by grid lines is also shown, with gray (dashed) and black (solid) lines corresponding to points having A and B as the last coordinate, respectively.

Figure 3. Illustration of R. An intersection of the slanted line with a grid line represents a single point in R, while passing through a grid point corresponds to two points in R.

We are interested in the track when it has traveled some distance $L=\rho n^{3/2} + O(n)\in{\mathbb{Z}}$ on the graph. This is represented by a distance of approximately $\rho n^{1/2}$ in the current grid, where each segment represents an arc of the cycle. Most of the analysis to follow holds for a generous range of the constant $\rho$ , but afterwards it will have to be tuned differently when applied to the upper and lower bounds on the mixing time.

Formally, we need the following linear set, illustrated in Figure 3:

(3) \begin{equation} R = \{(x,y,h) \in {\mathbb{R}}_+^2\times H \mid (x\in{\mathbb{Z}}_+,h=B) \textrm{ or } (y\in{\mathbb{Z}}_+,h=A),\ kx+(n-k)y=L\}.\end{equation}

Observe that the expression $kx+(n-k)y$ exactly represents the scaling needed for a segment corresponding to k or $n-k$ steps on the cycle, depending on the orientation. In particular, the current constraint with $L\in{\mathbb{Z}}$ ensures that points of $R\subset R_*$ properly map to vertices of the cycle graph, i.e. have appropriate rational and integer coordinates. Let us denote by $g\colon R\longrightarrow V$ the function that recovers the vertex of the graph given a point in R. For $r\in R$ let us denote by $E_r$ the event that the Markov chain reaches r. Observe that these present a mutually exclusive partitioning of the probability space (except for a null set where the movement of the Markov chain is bounded).

3.1. Exact expression for $E_r$ probabilities

The main goal of this section is to obtain ${\mathbb{P}}(E_r)$ . We develop a precise formulation for all $r\in R_*$ in Lemma 1, which, however, provides a formula that is hard to handle directly. Therefore, in the following section we look for simpler asymptotic bounds based on the current findings.

Let us examine how the Markov chain may reach r. The possibilities consist of a collection of paths from $X_0$ to r, each composed of unit grid segments, except possibly the first and last sections.

The transition probabilities at the hubs imply that after traversing an A segment there is a $\frac{3}{4}$ probability of moving along B and $\frac{1}{4}$ of taking another A, and vice versa. Indeed, notice that as long as moving happens between the hubs $\{a_k,b_{n-k}\}$ , by having all four Markov chain transition probabilities at $\frac{1}{4}$ within this set, after the first step the conditional distribution is uniform and stays so until moving forward on one of the arcs. Therefore, in total the chain either steps ahead instantly with probability $\frac{1}{2}$ or stays for one or more steps at the hubs, resulting in a uniform split of the remaining probability. Formally, first for the representation of the hubs as ${\mathbb{Z}}_+^2\times H$ the transition probabilities are

\begin{align*} {\mathbb{P}}((x,y,A),(x,y+1,B)) & = {\mathbb{P}}((x,y,B),(x+1,y,A)) = \tfrac 3 4, \\[5pt] {\mathbb{P}}((x,y,A),(x+1,y,A)) & = {\mathbb{P}}((x,y,B),(x,y+1,B)) = \tfrac 1 4.\end{align*}

We then need the straightforward extension for intermediate points of the segments, where the transition is deterministic from/to the hubs.

Clearly, any possible route can be encoded by the segments taken, thus by a word $w\in H^*$ , noting that the first and last segments might be incomplete when the initial and end points do not correspond to $a_k$ or $b_{n-k}$ . By the above, the probability of following such a word is determined by the number of changes, in total

\begin{align*} \frac{3^{|\{1\le i \le |w|-1 \,\mid\, w_i\neq w_{i+1}\}|}}{4^{|w|}}.\end{align*}

For a fixed $r=(x,y,h)\in R$ , let us define the preceding grid point on ${\mathbb{Z}}_+^2$ by decreasing in the h direction to get $r'=(x',y')$ :

\begin{align*} r' = (x',y') = \begin{cases} (\lceil x \rceil -1, y) & \text{ if } h=A,\\[5pt] (x, \lceil y \rceil -1) & \text{ if } h=B.\end{cases}\end{align*}

We will simply use x ^′, y ^′ by themselves if r is clear from the context.

Lemma 1. For any $r\in R_*$ , we have the following probability bound for reaching it:

(4) \begin{equation} {\mathbb{P}}(E_r) \ge \tfrac 1 4 \big[\mathrm{Binom}\big(x', \tfrac 3 4\big) * \mathrm{Binom}\big(y', \tfrac 1 4\big)\big](y') \ge \tfrac{1}{9}{\mathbb{P}}(E_r), \end{equation}

where Binom represents a binomial distribution, and $*$ indicates convolution.

Proof. For the moment, let us assume that $X(0)_H=A$ , $r_H=B$ , and $x',y'>0$ . The calculations for all other cases work similarly; we discuss the differences afterwards.

We need to gather all possible routes to r together with their probabilities. Assume that there were $2i+1$ changes of direction (it is certainly odd as a start on A ended on a B segment). This already determines that the probability of such a path is

\begin{align*} \bigg(\frac 3 4\bigg)^{2i+1} \bigg(\frac 1 4\bigg)^{x^{\prime}+y^{\prime}-2i}.\end{align*}

To achieve $2i+1$ changes of direction, we need to split the total of x ^′ full steps on A into $i+1$ parts, noting that a change may be valid after 0 steps due to the initialization $X(0)_H=A$ . Consequently, there are $\left( \substack{ x^{\prime} \\[3pt] i } \right)$ ways to do this. Similarly, there are $\left( \substack{ y^{\prime} \\[3pt] i } \right)$ possibilities to arrange the steps of B. Joining all the possible values of $2i+1$ we get

\begin{align*} {\mathbb{P}}(E_r) = \sum_{i=0}^{\infty} \left(\begin{array}{c}{x'}\\[2pt] {i}\end{array}\right) \left(\begin{array}{c}{y'}\\[2pt] {i}\end{array}\right) \bigg(\frac{3}{4}\bigg)^{2i+1} \bigg(\frac{1}{4}\bigg)^{x^{\prime}+y^{\prime}-2i}. \end{align*}

(The summation to $\infty$ is just for notational convenience – clearly there are only finitely many non-zero terms.) We may reformulate this as follows:

\begin{align*} {\mathbb{P}}(E_r) & = \sum_{i=0}^\infty \left(\begin{array}{c}{x'}\\[2pt] {i}\end{array}\right) \left(\frac 3 4\right)^{i+1} \left(\frac 1 4\right)^{x^{\prime}-i} \left(\begin{array}{c}{y'}\\[2pt] {y^\prime - i}\end{array}\right) \left(\frac 1 4\right)^{y^{\prime}-i} \left(\frac 3 4\right)^{i} \\[5pt] & = \tfrac 3 4 \big[\mathrm{Binom}\big(x',\tfrac 3 4\big) * \mathrm{Binom}\big(y', \tfrac 1 4\big)\big](y'). \end{align*}

For all the scenarios in terms of the orientation of the first and last segments, we can perform the same computation. Collecting all the similar expressions together we get:

(5) \begin{align} \!\! X(0)_H = A,\ r_H = B \quad\Rightarrow\quad {\mathbb{P}}(E_r) & = \tfrac 3 4 \big[\mathrm{Binom}\big(x', \tfrac 3 4\big) * \mathrm{Binom}\big(y', \tfrac 1 4\big)\big](y'), \qquad\quad \end{align}

(6) \begin{align} X(0)_H = A,\ r_H = A \quad\Rightarrow\quad {\mathbb{P}}(E_r) & = \tfrac 3 4 \big[\mathrm{Binom}\big(x'+1, \tfrac 3 4\big) * \mathrm{Binom}\big(y'-1, \tfrac 1 4\big)\big](y'), \end{align}

\begin{align*} \!\! X(0)_H = B,\ r_H = B \quad\Rightarrow\quad {\mathbb{P}}(E_r) & = \tfrac 3 4 \big[\mathrm{Binom}\big(x'-1, \tfrac 3 4\big) * \mathrm{Binom}\big(y'+1, \tfrac 1 4\big)\big](y'), \nonumber \\[5pt] X(0)_H = B,\ r_H = A \quad\Rightarrow\quad {\mathbb{P}}(E_r) & = \tfrac 3 4 \big[\mathrm{Binom}\big(x', \tfrac 3 4\big) * \mathrm{Binom}\big(y', \tfrac 1 4\big)\big](y'). \nonumber \end{align*}

For our convenience we want to avoid case splitting. Observe that for each combination we get the probability of interest through checking the sum of $x'+y'$ independent bits for a certain total value, with very minor differences between the distribution of the bits. For instance, when comparing (5) and (6), we have, for any $s \in [0,1,\ldots, x'+y']$ ,

\begin{align*} \frac 1 3 \le \frac{\big[\mathrm{Binom}\big(x'+1, \frac 3 4\big) * \mathrm{Binom}\big(y'-1, \frac 1 4\big)\big](s)} {\big[\mathrm{Binom}\big(x', \frac 3 4\big) * \mathrm{Binom}\big(y', \frac 1 4\big)\big](s)} \le 3, \end{align*}

as the two bit-streams can be perfectly coupled except for a single bit of probability $\frac 3 4$ being coupled to a bit of probability $\frac 1 4$ . Using the same comparison for the other cases with the reference (5) and accepting this error margin, we get the overall bounds

\begin{align*} {\mathbb{P}}(E_r) & \ge \tfrac 1 4 \big[\mathrm{Binom}\big(x', \tfrac 3 4\big) * \mathrm{Binom}\big(y', \tfrac 1 4\big)\big](y'), \\[5pt] \tfrac 1 3 {\mathbb{P}}(E_r) & \le \tfrac 3 4 \big[\mathrm{Binom}\big(x', \tfrac 3 4\big) * \mathrm{Binom}\big(y', \tfrac 1 4\big)\big](y'), \end{align*}

which combine to give the statement of the lemma. This is now valid irrespective of direction. Even more, this final inequality holds true when $x'=0$ or $y'=0$ (although we will not use it).

We would like to emphasize that using the two binomial distributions and evaluating their convolution at one point provides the probability for a single $E_r$ ; different parameters appear for every other element of R.

In the next subsection we aim to bound this in a simpler form that sheds light on the magnitude of the expressions just obtained. For that purpose we restrict the analysis to the region of interest R that is at the prescribed distance, and, even further, to a central region where a concentration effect will provide a non-negligible probability of arriving there.

3.2. Simplified estimates of $E_r$ probabilities

We will provide estimates of ${\mathbb{P}}(E_r)$ for points which are close to the diagonal, where we can hope a large number of high-probability tracks will pass through leading to some concentration, which intuitively means approximately equal numbers of A and B. Formally, define

\begin{align*} R_0 = \{r \in R \mid |x'-y'| \le \sqrt{\rho}n^{1/4}\}.\end{align*}

By the definition of R in (3) we get $\min(x',y')n \le L \le \max(x',y')n$ , which ensures that, for any $r\in R_0$ ,

(7) \begin{equation} x',y' \in \big[\rho n^{1/2} - \sqrt{\rho}n^{1/4} + O(1), \, \rho n^{1/2} + \sqrt{\rho}n^{1/4} + O(1)\big].\end{equation}

Lemma 2. There exists a constant $\gamma_1>0$ such that, for n large enough and any point $r\in R_0$ ,

(8) \begin{equation} {\mathbb{P}}(E_r) \ge \frac{\gamma_1}{\sqrt{\rho}n^{1/4}}. \end{equation}

Clearly this is what we would expect from central limit theorem (CLT) asymptotics after approximately $\rho n^{3/2}$ steps, and such bounds are widely available for simple binomial distributions. Here is one possible way to confirm the claim for our non-homogeneous case.

Proof. Let $Q = \mathrm{Binom}\big(x', \frac 3 4\big) * \mathrm{Binom}\big(y', \frac 1 4\big)$ , the distribution appearing in (4). It can be viewed as the sum of $x'+y'$ independent indicators. We will approximate Q with a Gaussian variable in a quantitative way using the Berry–Esseen theorem [3, 8].

In terms of expectation, we clearly have $(3x'+y')/4$ in total. For an indicator with probability $\frac 1 4$ the variance is $\frac{3}{16}$ , and we get the same for the indicator with probability $\frac 3 4$ due to symmetry. Consequently, we may consider the approximation

\begin{align*} Q \approx {\mathcal{N}}\bigg(\frac{3x'+y'}{4},\frac{3x'+3y'}{16}\bigg). \end{align*}

The absolute third moment after centralizing is $\frac{15}{128}$ for both types of indicator, which is used in the approximation bound.

Denoting by $F_Q$ and $F_{\mathcal{N}}$ the cumulative distribution functions of Q and the properly scaled Gaussian above, the Berry–Esseen theorem (for variables that are not identically distributed) ensures

(9) \begin{equation} \sup_{\xi\in{\mathbb{R}}} |F_{Q}(\xi) - F_{{\mathcal{N}}}(\xi)| \le \beta_1 \frac{\frac{15}{128}(x'+y')}{\big(\frac{3}{16}(x'+y')\big)^{3/2}} = \frac{\beta_2}{(x'+y')^{1/2}}, \end{equation}

where $\beta_1>0$ is the global constant of the theorem, leading to a constant $\beta_2>0$ when combined with the numerical values coming from the second and third moments involved.

Note that here we are comparing an independent sum and a Gaussian with matching first and second moments rather than a centered and normalized sum with a standard Gaussian as originally stated for the Berry–Esseen theorem, but joint shifting and scaling does not change the difference of the cumulative distribution functions nor the bounding quantity.

We now introduce the normalized distribution $\tilde{Q}$ by

\begin{align*} \tilde{Q}\bigg(\bigg(C-\frac{3x'+y'}{4}\bigg)\frac{4}{\sqrt{3x'+3y'}\,}\bigg) = Q(C) \end{align*}

for any measurable set C, which is then approximated by the standard Gaussian distribution $\Phi$ (but is still a discrete distribution). This definition implies that in (4) we need the value of $\beta_3 = \tilde{Q}(\{\alpha\})$ , where $\alpha = {\sqrt{3}(y'-x')}/{\sqrt{x'+y'}}$ . Observe that, by the definition of $R_0$ and thus (7) we have $|\alpha|<\sqrt{3/2}+O(n^{-1/8})<3/2$ for n large enough. Define the intervals $I_- = \big[{-}2,-\frac 3 2\big]$ , $I_+ = \big[\frac 3 2, 2\big]$ . Recall that binomial distributions are log-concave, and so is their convolution Q, and its affine modification $\tilde{Q}$ . Consequently, for any grid point the probability is at least all those that precede it, or at least all those that are after it. In particular, $\beta_3$ is bounded below by all the (grid point) probabilities of $I_-$ or $I_+$ . Simplifying further, we can take the average probabilities on the intervals; the lower will be a valid lower bound for $\beta_3$ .

By the Berry–Esseen estimate (9) for the overall probabilities on the intervals we have

\begin{align*} q_-= \tilde{Q}(I_-) = \Phi\big(\big[{-}2, -\tfrac 3 2\big]\big) + O(n^{-1/4}), \qquad q_+ = \tilde{Q}(I_+) = \Phi\big(\big[\tfrac 3 2, 2\big]\big) + O(n^{-1/4}). \end{align*}

We estimate the number of grid points in the two intervals. To compute the average we refer back to the unnormalized distribution Q where we have to count the integers in the corresponding intervals, considering the scaling used. As an upper bound m for the number of contained grid points we get

\begin{align*} m \le \bigg\lfloor \frac 1 2 \frac{\sqrt{3x'+3y'}}{4}\bigg\rfloor +1 \le \frac{\sqrt{6\rho}}{8}(n^{1/4}+O(n^{1/8}))+1 \le \frac 1 2 \sqrt{\rho}n^{1/4} +O(n^{1/8}). \end{align*}

Combining our observations and estimates we can bound by the averages:

\begin{equation*} \beta_3 \ge \frac{\min(q_-,q_+)}{m} \ge \frac{\Phi([3/2, 2]) + O(n^{-1/4})}{(1/2) \sqrt{\rho}n^{1/4} + O(n^{1/8})} = \frac{\beta_4}{\sqrt{\rho}n^{1/4}} + O(n^{-1/8}). \end{equation*}

Finally, plugging this bound on $\beta_3$ into (4), we arrive at

\begin{equation*} {\mathbb{P}}(E_r) \ge \frac{\gamma_1}{\sqrt{\rho}n^{1/4}}, \end{equation*}

for any $0<\gamma_1<\beta_4/4$ and n large enough, which matches the claim of the lemma.

4. Mapping the grid to the cycle

In the previous section, using the grid we abstractly identified points R at appropriate distance from the starting position, and also points $R_0\subseteq R$ which are reached with non-negligible probabilities. As the next step, we want to understand what these points represent on the original cycle. If we are able to show that these points are sufficiently spread out, it will serve as a good foundation to establish mixing. Without loss of generality we assume $k\le n/2$ .

Lemma 3. $\sqrt{\rho}n^{1/4}+O(1) \le |R_0| \le 4\sqrt{\rho}n^{1/4}+O(1)$ .

Proof. For the moment, we use the notation $\tilde{L}=L/n=\rho n^{1/2}+O(1)$ . Setting both x and y to $\tilde{L}$ would solve the defining equation $kx+(n-k)y=L$ . Thus, for any integer $x \in \big[\tilde{L}-\frac{1}{2}\sqrt{\rho}n^{1/4}+1, \tilde{L}+\frac{1}{2}\sqrt{\rho}n^{1/4}-1\big]$ there is a corresponding y in the same interval that solves the defining equation. Notice that, by the assumption $k \le n-k$ , the y we get will differ from the center value no more than x. Therefore, $|x-y|\le \sqrt{\rho}n^{1/4}-2$ , which is enough to ensure the pair accompanied by a B being in $R_0$ . The number of integers in the given interval for x confirms the lower bound.

Adjusting this argument, check in the interval $x \in [\tilde{L} - \sqrt{\rho}n^{1/4}, \tilde{L} + \sqrt{\rho}n^{1/4}]$ , $x \in {\mathbb{Z}}$ , with approximately double width, which is a necessary condition for being in $R_0$ and of the form $(\cdot,\cdot,B)$ . There will be at most one such point in $R_0$ for each x, so $2\sqrt{\rho}n^{1/4}+O(1)$ in total. Now, counting the points on horizontal grid lines (collecting $(\cdot,\cdot,A)$ points), for any $y \in [\tilde{L} - \sqrt{\rho}n^{1/4}, \tilde{L} + \sqrt{\rho}n^{1/4}]$ , $y \in {\mathbb{Z}}$ , there will be at most one matching point in $R_0$ again. Adding up the two cases we get the upper bound.

It will be more convenient to handle a set of points of known size, so let $R_1\subseteq R_0$ be a subset of size $\sqrt{\rho}n^{1/4}$ (or maybe O(1) less) of the elements in the middle.

Figure 4. Possible transitions depicted as $U\rightarrow U'$ while scanning through $R_1$ .

We want to convert our grid representation to the cycle and acquire the image of $R_1$ , i.e.

\begin{align*} V_1 = \{g(r) \mid r\in R_1\};\end{align*}

recall that g is the mapping from the grid points and lines to the cycle. To understand this set, we scan through the elements of $R_1$ , starting with the one with the lowest x and increasing (taking direction A before B when passing through a grid point), and follow where they map on the cycle. When switching from one point, U, to the next, U ^′, we may encounter the following configurations, as shown in Figure 4:

1. (i) We see that the final few l steps (out of L) start on the B arc for U and on the A arc for U ^′. Consequently, U ^′ can be reached from U by exactly k counter-clockwise steps on the cycle.

2. (ii) Here, we almost reach the next grid point; some l steps are missing on the A arc for U and also l steps are missing on the B arc for U ^′. This means, again, that U ^′ can be reached from U by exactly k counter-clockwise steps on the cycle.

3. (iii) Here, we are on the B arc for both U and U ^′, but we had one more horizontal A segment for U ^′ (representing k steps) which is missing from the height. Therefore, we get the same relation: U ^′ can be reached from U by exactly k counter-clockwise steps on the cycle.

4. (iv) Note that case (iv) cannot happen due to our assumption of $k \le n/2$ .

5. (v) Passing through a grid point can be treated as a special case of either (i) or (ii), with the same consequence.

To sum up, we can generate the set $V_1\subset V$ on the cycle corresponding to $R_1$ by finding the first vertex, then taking jumps of $-k$ (modulo n) for $|R_1|-1$ more steps. To proceed, we want to ensure the elements of $V_1$ are sufficiently spread out.

Lemma 4. There exist constants $\gamma_{2} > \frac 1 2$ and $\gamma_3 > 0$ such that the following holds for large enough n. For a uniform choice of $k\in [2,3,\ldots,n-2]$ , with probability at least $\gamma_3$ , we have, for all $r,r'\in R_1$ , $r \neq r'$ ,

(10) \begin{equation} |g(r)-g(r')|\geq \frac{\gamma_{2}}{\sqrt{\rho}\,} n^{3/4}. \end{equation}

Proof. We use $\gamma_{2}$ as a parameter for now, which we will specify later. We consider a uniform choice $k\in [1,2,\ldots,n]$ for convenient calculations; clearly this does not change the probability asymptotically.

Two elements of $R_1$ map close if, after some repetitions of the k-jumps, we get very close to the start (after a number of full turns). More precisely, the condition is violated if and only if there exists $1\le m \le |R_1|-1$ such that $|mk| < ({\gamma_{2}}/{\sqrt{\rho}}) n^{3/4}$ . Our goal is to have a k so that this does not happen. For a fixed m this excludes k from the intervals

\begin{align*} \bigg(\frac{in - \frac{\gamma_{2}}{\sqrt{\rho}\,} n^{3/4}}{m}, \frac{in + \frac{\gamma_{2}}{\sqrt{\rho}\,} n^{3/4}}{m}\bigg),\qquad i=0,1,\ldots,m-1. \end{align*}

To simplify our calculations we treat these intervals as real intervals on the cycle (rather than integer intervals). The length and number of integers contained differ by at most one; we will correct for this error at the end.

We need to merge these intervals for all $1\le m \le |R_1|-1$ . We imagine doing this by collecting the intervals as increasing m. Observe that if $\gcd(i,m)=c>1$ , then we already covered the interval around $({in})/{m}$ when encountering $[{(i/c)n}]/({m/c})$ with a wider interval before. That is, we only have to count those i where $\gcd(i,m)=1$ , having only $\varphi(m)$ of them, $\varphi$ being the classical Euler function. Therefore, combining their count and the length of a single interval, the total newly covered area at step m is at most

\begin{align*} \frac{2\gamma_{2}}{\sqrt{\rho}\,} n^{3/4} \frac{\varphi(m)}{m}. \end{align*}

Once we add these up, and use the summation approximation [15], we get

(11) \begin{equation} \frac{2\gamma_{2}}{\sqrt{\rho}\,} n^{3/4}\sum_{m=1}^{|R_1|-1}\frac{\varphi(m)}{m} = 2\gamma_{2}\frac{6}{\pi^2}n + O(n^{3/4}\log n), \end{equation}

knowing that $|R_1| = \sqrt{\rho}n^{1/4}+O(1)$ . When we switched from integer counts to approximation by interval lengths, the total error is at most one per interval, i.e. $\sum_{m=1}^{|R_1|-1} m = O(n^{1/2})$ , which is negligible compared to the quantities of (11). Consequently, (11) is an upper bound on the number of k that should be excluded. Let us therefore choose $\gamma_{2} > \frac 1 2$ so that the coefficient of n above is strictly less than 1. Then, there is still a strictly positive probability of picking a good k, in particular $\gamma_3 = 1 - ({12\gamma_{2}})/{\pi^2}-\varepsilon$ is adequate for any small $\varepsilon > 0$ .

5. Including diffusive behavior

So far we have understood the position of the chain after L moves from the first grid point. Now we want to analyze the true Markov chain dynamics where randomized moving or pausing is included. In $V_1$ we have a large number of positions, hopefully different and separated enough on the cycle, and we can bound the probability of reaching the corresponding elements in $R_1$ on the grid. Our goal is to show that with the randomization of moving, a diffusive phenomenon enters, so that vertices near $V_1$ will be likely to be reached.

For technical reasons, we want to avoid points in $V_1$ that are very close to the hubs, so we define

(12) \begin{align} V_2 &= \{v\in V_1 \mid |v-k|,|v-n| > 4\sqrt{\rho}n^{3/4}\sqrt{\log n}\},\nonumber\\[2pt] W &= \{ w \in V \mid \mathrm{there\ exists}\ v\in V_2,\ |w-v| < \gamma_{2}\sqrt{\rho} n^{3/4}/2\},\\[2pt] R_2 &= \{r\in R_1 \mid g(r) \in V_2\}.\nonumber \end{align}

We would like to emphasize that in the favorable case when (10) holds (ensured with positive probability by Lemma 4), we have $|V_2|, |R_2| = \sqrt{\rho}n^{1/4} + O(\sqrt{\log n})$ , and when $\rho\le 1$ this also implies $|W| = \gamma_{2} \rho n + O(n^{3/4}\sqrt{\log n})$ .

At most vertices of the cycle, a Geo $\big(\frac 1 2\big)$ distribution controls when to step ahead, so let us choose some $T = 2\rho n^{3/2} + O(n) \in 2{\mathbb{Z}}$ and analyze X(T). Oversimplifying the situation at first, in T steps the chain travels $T/2$ in expectation, O(n) to reach the origin grid point, and $\rho n^{3/2}+O(n)$ afterwards, which is exactly the case analyzed before. Assuming this constant speed, we have approximately $\sqrt{\rho} n^{1/4}$ expected endpoints in $R_2\subseteq R_0$ with probability uniformly bounded below to be hit by Lemma 2. We will have a diffusion of approximately $\sqrt{\rho}n^{3/4}$ around each of them, which together will provide a nicely spread-out distribution.

However, there are some non-trivial details hidden here. The most important caveat is that when visiting the hubs, the distribution of the time spent is not independent of the direction taken. In fact, when arriving at a hub, say at vertex $a_k$ , with probability $\frac 1 2$ there is a single step, going to $b_1$ . Otherwise, in some loops or some loop steps, jumps are taken between the hubs before moving on, which tells us that with probability $\frac 1 4, \frac 1 4$ the chain continues to $a_1,b_1$ in $1+\mathrm{Geo}\big(\frac 1 2\big)$ steps. Let us combine all the heuristics and work out the details in a formally precise way.

We are going to describe a procedure to generate the Markov chain and the position X(T). If X(0) is $\lambda$ steps before one of the hubs, thus the origin grid point, fix $L=T/2-\lambda = \rho n^{3/2}+O(n)$ , and define R with this value in (3). Assume we are given an infinite independent and identically distributed series of fair coin tosses which may either say ‘go’ (1) or ‘do nothing’ (0). We perform the following steps.

• Choose the exit point $r\in R$ , with appropriate probability ${\mathbb{P}}(E_r)$ .

• Choose one of the possible tracks $\xi$ reaching r (with the appropriate conditional probability).

• Generate a series of coin tosses $c_0$ of length $T-(x'+y'+1)$ , which is the major part of the movement of the chain.

• Complement the above series depending on the track. Following the Markov chain using the beginning of $c_0$ , when we reach a hub where the direction should be continued according to $\xi$ (AA or BB), insert an extra 0 symbol (correcting for the $1+\mathrm{Geo}\big(\frac 1 2\big)$ waiting time distribution there). Similarly, when we reach a hub where the direction changes (AB or BA), with probability $\frac 2 3$ insert a 1 (meaning an instant step), with probability $\frac 1 3$ insert a 0 (for the $1+\mathrm{Geo}\big(\frac 1 2\big)$ case).

• If we encounter a grid point further than r, we freely choose the direction together with the inserted symbol with probabilities $\frac 1 4, \frac 1 2, \frac 1 4$ for the three cases we had.

Let the elongated series be $c_1$ , and the sequence of only the added symbols be $c_h$ . We use the notation $|c_0|$ for the length of $c_0$ and $\sum(c_0)$ for the number of 1s in $c_0$ (and similarly for the other sequences). Let us also introduce $\tau = |c_1|$ . Therefore, at the end of the procedure above we arrive at $X(\tau)$ . More importantly, $\tau$ matches T very well, as stated next.

Lemma 5. For $r\in R_2$ , ${\mathbb{P}}(\tau = T) = 1 - O(n^{-4})$ .

Proof. In $c_0$ , for the number of 1 symbols we have

\begin{align*} \bigg|\sum(c_0)-(L+\lambda)\bigg| \le \bigg|\sum(c_0)-\tfrac{1}{2}(T-(x'+y'+1))\bigg| + \bigg|\tfrac{1}{2}(T-(x'+y'+1))-(L+\lambda)\bigg|. \end{align*}

The second term on the right-hand side is deterministic and $O(n^{1/2})$ by the definitions. For the term before, we can use standard tail probability estimates for the binomial distribution (based on Hoeffding’s inequality). Merging the two error terms, we get

(13) \begin{equation} {\mathbb{P}}\bigg(\bigg|\sum(c_0)-(L+\lambda)\bigg| > 3\sqrt{\rho}n^{3/4}\sqrt{\log n}\bigg) = O(n^{-4}). \end{equation}

Let us denote this bad event of the left side above by $\mathcal{B}$ for future use. Assume that this event does not occur, so $\sum(c_0)$ is within the error bound $3\sqrt{\rho}n^{3/4}\sqrt{\log n}$ . This means that the Markov chain takes the first $\lambda$ steps to the origin and then approximately L steps within the stated bounds.

By the definition of $R_2$ , this concentration means that even only considering the $c_0$ steps we reach the grid line segment where r lies. On the way, we pass through $x'+y'+1$ hubs, which results in $x'+y'+1=O(n^{1/2})$ entries in $c_h$ . Conversely, inserting these $O(n^{1/2})$ steps into $c_0$ , the upper bound ensures that we will not reach the next grid point (or the hub once more, in other words). Consequently, $|c_h|=x'+y'+1$ .

In this case we have $\tau = |c_1| = |c_0| + |c_h| = T$ , which is the preferable case we wanted to show; the exceptional probability is controlled by (13), which matches the claim.

Now we are ready to bound the probability of the Markov chain to reach the points of the set highlighted by W.

Lemma 6. For any $w\in W$ , ${\mathbb{P}}(X(T)=w) \ge {\gamma_4}/({\rho n})$ for an appropriate global constant $\gamma_4>0$ .

Proof. By the definition of W there is a $v = g(r)\in V_2$ with $|v-w| \le \frac{1}{2}\gamma_{2}\sqrt{\rho} n^{3/4}$ (if multiple, we choose one). We use the procedure above to actually bound the probability for $X(\tau)$ , but by Lemma 5 we know this is correct up to an $O(n^{-4})$ error, which is enough for our case. In the process, let us consider $E_r$ chosen and also pick some temporarily fixed track $\xi$ reaching it, and condition on them.

With these conditions, let us analyze the dependence structure of the step sequences. For $c_1$ , the positions of the additions strongly depend on $c_0$ . However, we know exactly which hubs and turns we are going to take, which means $c_h$ is independent of $c_0$ (assuming $\bar{\mathcal{B}}$ ); only their interlacing depends on both.

Now, first drawing and fixing $c_h$ we know by $\sum(c_h)$ precisely how many 1s we need from $c_0$ to exactly hit w (still conditioning on $E_r$ and $\xi$ ). Let this number be s, for which we clearly have $|s-\rho n^{3/2}| \le \gamma_{2}\sqrt{\rho} n^{3/4}/2 + O(n^{1/2})$ . The length of $c_0$ is $T'=T-(x'+y'+1) = T + O(\sqrt{n})$ . We have to approximate this binomial probability of 1s in $c_0$ . This is a tedious calculation based on the Stirling formula; we refer to [14], where it is shown that

\begin{align*} \left(\begin{array}{c}{T'}\\[2pt] {s}\end{array}\right) = (1+o(1))\frac{2^{T'}}{\sqrt{T'\pi/2}\,} \exp\bigg({-}\frac{(T'-2s)^2}{2T'}\bigg), \end{align*}

if $|{T'}/2-s| = o({T'}^{2/3})$ , which clearly holds in our case. Substituting the variables, we get the bound

\begin{align*} \left(\begin{array}{c}{T'}\\[2pt] {s}\end{array}\right) \frac{1}{2^{T'}} \ge (1+o(1)) \frac{1}{\sqrt{\pi\rho}n^{3/4}} \exp\bigg({-}\frac{\gamma_{2}^{2}}{4}+O(n^{-1/4})\bigg) \ge \frac{\beta_1}{\sqrt{\rho}n^{3/4}}, \end{align*}

for some constant $\beta_1>0$ and n large enough. Thus, for the conditional probability of interest we get

\begin{align*} {\mathbb{P}}(X(T)=w \mid E_r,\xi,c_h) \ge \frac{\beta_1}{\sqrt{\rho}n^{3/4}} - {\mathbb{P}}(\mathcal{B}) \ge \frac{\beta_2}{\sqrt{\rho}n^{3/4}} \end{align*}

for any constant $\beta_1 > \beta_2 >0$ and n large enough.

Observe that we have the same lower bound for ${\mathbb{P}}(X(T)=w \mid E_r)$ , as it is a mixture of the conditional probabilities above, so we can average out through $\xi$ and $c_h$ . Finally, combining with (8) we arrive at

(14) \begin{equation} {\mathbb{P}}(X(T)=w) \geq {\mathbb{P}}(X(T)=w \mid E_r){\mathbb{P}}(E_r) \ge \frac{\gamma_4}{\rho n}, \end{equation}

with an appropriate constant $\gamma_4 >0$ .

6. Global mixing

We now turn to evaluating the mixing metrics of our Markov chain. In order to establish the upper bound on the mixing time initially claimed in Theorem 1, we fix $\rho=1$ and $T=2\lceil\rho n^{3/2}\rceil$ for this section and use previous results using these parameters. We will drop X from the indices and arguments in (1) and (2) when clear from the context.

Our current reasoning would only prove a total variation decrease down to a certain constant amount but no further, so we need to add one more step to reach any ${\varepsilon}$ . An alternative to d(t) compares the distribution of the Markov chain when launched from two different starting points: $\overline{d}(t) \;:\!=\; \sup_{X^1(0),X^2(0)\in V} \|{\mathcal{L}}(X^1(t))-{\mathcal{L}}(X^2(t))\|_{\rm TV}$ . It is known how this compares with d(t), in particular $d(t) \le \overline{d}(t) \le 2d(t)$ , and moreover this variant has the advantage of being submultiplicative, $\overline{d}(s+t)\le\overline{d}(s)\overline{d}(t)$ ; see [13, Chapter 4]. We can quantify this distance for our problem as follows.

Lemma 7. Assume that n is large enough and k is such that (10) holds. Then we have

(15) \begin{equation} \overline{d}(T) \le 1 - \gamma_5 , \end{equation}

for some global constant $\gamma_5 \gt 0$ .

Proof. Fix two arbitrary starting vertices for $X^1(0)$ and $X^2(0)$ , and denote the distribution of the two chains at time T by $\sigma^1,\sigma^2$ . Simple rearrangements yield

(16) \begin{align} \begin{aligned} \|\sigma^1 - \sigma^2\|_{\rm TV} & = \frac 1 2 \sum_{v\in V} |\sigma^1(v) - \sigma^2(v)| \\[5pt] & = \frac 1 2 \sum_{v\in V} (\sigma^1(v) + \sigma^2(v) - 2\min(\sigma^1(v), \sigma^2(v))) \\[5pt] & = 1 - \sum_{v\in V} \min(\sigma^1(v), \sigma^2(v)). \end{aligned} \end{align}

For both realizations, in the definitions of (12) we get a subset of vertices W. Denote the two realizations by $W^1,W^2$ , and notice that there must be a considerable overlap; in particular,

\begin{align*} |W^1\cap W^2| \ge |W^1|+|W^2|-n = (2\gamma_{2} -1)n + O(n^{3/4}\sqrt{\log n}) \ge \beta n \end{align*}

for some $\beta > 0$ and n large enough, relying on the fact that $\gamma_{2} > \frac 1 2$ . By Lemma 6, for any $w \in W^1\cap W^2$ we have both $\sigma^1(w),\sigma^2(w) \geq \gamma_4/n$ . Substituting this back into (16), we get $\|\sigma^1 - \sigma^2\|_{\rm TV} \leq 1 - (\beta n) ({\gamma_4}/{n}) = 1 - \gamma_5$ , with $\gamma_5 = \beta\gamma_4$ . This upper bound applies for any two starting vertices of $X^1,X^2$ , and therefore the claim follows.

We just need the final touch to prove Theorem 1.

Proof of Theorem 1. Using Lemma 4, we have a spread-out collection in $V_2$ as stated in (10) with probability at least $\gamma_3\;=\!:\;\gamma$ . In this case, we can apply Lemma 7. Fix

\begin{align*} T^* = \bigg\lceil \frac{\log {\varepsilon}}{\log (1-\gamma_5)}\bigg\rceil T. \end{align*}

Substituting (15) and using the basic properties of $d,\overline{d}$ , we get

\begin{align*} d(T^*) \le \overline{d}(T^*) \le \overline{d}(T)^{\lceil ({\log {\varepsilon}})/({\log (1-\gamma_5)})\rceil} \le (1-\gamma_5)^{\lceil ({\log {\varepsilon}})/({\log (1-\gamma_5)})\rceil} \le {\varepsilon}. \end{align*}

Consequently, $t_{\rm mix}({\varepsilon}) \le T^*$ . On the other hand,

\begin{align*} T^* = \bigg\lceil \frac{\log {\varepsilon}}{\log (1-\gamma_5)}\bigg\rceil T = \bigg\lceil \frac{\log {\varepsilon}}{\log (1-\gamma_5)}\bigg\rceil 2\lceil n^{3/2}\rceil \le \gamma' n^{3/2} \log\frac{1}{{\varepsilon}}, \end{align*}

for an appropriate constant $\gamma'>0$ and n large enough. Together with the previous calculation, this confirms the theorem.

7. Lower bound

Our goal is to have a universal lower bound, so our viewpoint has to be altered. In this section we fix $\rho = \gamma_4/2$ . To highlight the theme to follow, Lemma 6 would tell us that at elements of W there is at least $2/n$ probability of the Markov chain arriving, and thus the total variation can be bounded below by collecting these $1/n$ increments compared to the uniform distribution; as W ‘should’ have size approximately $\gamma_{2}\rho$ , we would get a constant-order lower bound.

We will need multiple refinements since, for general k, for all edge selections we have no information on the size of W, and there might be significant overlaps, multiplicities when defining $V_1$ or W; we do not have the comfort based on Lemma 4. It is key for completing the proof to be able to handle this.

We know $|R_1|=\sqrt{\rho}n^{1/4} + O(1)$ , but we have no size estimates on $|R_2|,|V_2|$ . For the technical conditions needed, as they were included in the definitions in (12), similarly for these constraints let the set of interest be

\begin{align*} I = \{v\in V \mid |v-k|,|v-n| > 4\sqrt{\rho}n^{3/4}\sqrt{\log n}\}.\end{align*}

For the moment, we cannot guarantee that most of $R_1$ maps into I. In order to change this, we start slightly increasing the target time and distance to shift these points, hopefully mostly into I. We define $T^i = 2\lceil \rho n^{3/2} \rceil + 2i$ and $L^i = \lceil \rho n^{3/2} \rceil - \lambda + i$ for $i=0,1,\ldots,n-1$ . Accordingly, there is an evolution $R^i$ and $R_0^i$ . Recall that $\lambda$ corresponds to the position of X(0), which is arbitrary, but we consider it as fixed.

For $R_1^i$ (together with $V_1^i$ ), we investigate this evolution from the perspective of the individual points. We can verify that a valid interpretation is that every $r=(x,y,h)\in R_1^0$ performs a zigzag away from the origin along the grid lines, stopping just before $(x+1, y+1,h)$ , turning at both grid points it passes along the way. Indeed, during the move, $|x'-y'|$ changes by at most 1, so we always get the centermost $\sqrt{\rho}n^{1/4}+O(1)$ points with the smallest $|x'-y'|$ . This defines $R_1^i$ up to edge effects, which we may encounter, but only at the extremal points of $R_1^i$ . This process is illustrated in Figure 5.

Figure 5. Evolution of the points of $R_1^i$ with the increase of i. Two such zigzag paths are depicted.

Observe that such a zigzag corresponds to walking around the cycle exactly once. This will allow us to conveniently calculate the total number of hits to I by $V_1^0,\ldots,V_1^{n-1}$ . More precisely (to account for multiplicities), we are interested in $M=\sum_{i=0}^{n-1} \sum_{r\in R_1^i} {\textbf{1}}_I (g(r))$ . By the previous argument, we know that along each point the number of hits is exactly $ |I| $ , except maybe near the edges. Thus, we get $M \ge |R_1|\cdot |I| - O(n)$ . Comparing the two while dividing by n, we get

\begin{align*} \frac{1}{n} \sum_{i=0}^{n-1} \sum_{r\in R_1^i} {\textbf{1}}_I (g(r))\ge |R_1|\frac{|I|}{n}-O(1)\ge \frac{|R_1|}{2}.\end{align*}

Consequently, there has to be a term of the average on the left-hand side larger than the right-hand side: $\sum_{r\in R_1^i} {\textbf{1}}_I (g(r)) \ge \frac{1}{2}|R_1|$ . Let us take and fix such an index i from now on. Define the analogous sets as before:

\begin{align*} R_2^i &= \{r\in R_1^i \mid g(r)\in I\},\\[5pt] W^i &= \{w\in V \mid \mathrm{there\ exists}\ r\in R_2^i, |g(r)-w| \le \gamma_{2}\sqrt{\rho}n^{3/4}/2\}.\end{align*}

We now formulate an extension of Lemma 6.

Corollary 1. For any $r\in R_2^i$ , $w\in W^i$ such that $|g(r)-w| \le \gamma_{2}\sqrt{\rho}n^{3/4}/2$ , we have

\begin{equation*} {\mathbb{P}}(X(T^i)=w, E_r) \ge \frac{\gamma_4}{\rho n}, \end{equation*}

for the same global constant $\gamma_4 \gt 0$ as before.

Proof. This is actually what happens under the hood in the proof of Lemma 6; there, the choice of r is given by the structure W and the extra knowledge on $E_r$ is discarded at the end in (14). Now there might be multiple values of r corresponding to the same w due to overlaps.

Proof of Theorem 2. We want to bound $d(T^i)$ , with the i carefully chosen above. By only analyzing the case of the starting point fixed above, we get a lower bound on $d(T^i)$ . We need to estimate the total variation distance:

\begin{align*} \bigg\|{\mathcal{L}}(X(T^i))-\frac{{\textbf{1}}}{n}\bigg\|_{\rm TV} = \frac 1 2 \sum_{v\in V} \bigg|P(X(T^i)=v)-\frac 1 n \bigg|. \end{align*}

Note that for any $w\in W^i$ there is a corresponding r nearby to apply Corollary 1, and with the choice of $\rho$ at the beginning of the section we get $P(X(T)=w)\ge 2/n$ . That is, these terms in the sum are positive without the absolute value. We drop all other values for a lower bound. Thus, we get

\begin{align*} \bigg\|{\mathcal{L}}(X(T^i))-\frac{{\textbf{1}}}{n}\bigg\|_{\rm TV} \ge \frac 1 2 \sum_{w\in W^i}\bigg(P(X(T^i)=w)-\frac 1 n\bigg)\ge \frac 1 2 \sum_{r,w} \frac 2 n - \frac 1 2 |W^i| \frac 1 n. \end{align*}

In the first term we may include all compatible pairs of r,w for which Corollary 1 can be applied. Recall that $|R^i_2| \ge \sqrt{\rho}n^{1/4}/2 + O(1)$ , each element compatible with a $\gamma_{2} \sqrt{\rho}n^{3/4} + O(1)$ number of ws.

For the second term being subtracted, we may count very similarly starting from $R^i_2$ and looking for compatible pairs. This time, however, the multiplicity does not add up as we need the size of the set, but we want an upper bound for this term anyway. In total, we get

\begin{align*} \bigg\|{\mathcal{L}}(X(T^i))-\frac{{\textbf{1}}}{n}\bigg\|_{\rm TV} & \ge \frac 1 n |R^i_2| \big({\gamma_{2}}{\sqrt{\rho}} n^{3/4} + O(1)\big) - \frac 1 {2n} |R^i_2| \big({\gamma_{2}}{\sqrt{\rho}} n^{3/4} + O(1)\big)\\[5pt] & \ge \frac {\gamma_{2}\rho} 4 + O(n^{-1/4}). \end{align*}

As $d(\!\cdot\!)$ is non-increasing, for the constants of the theorem we may choose $\gamma^*=2\rho=\gamma_4$ and any ${\varepsilon}^*<\gamma_{2}\rho/4 = \gamma_{2}\gamma_4/8$ . With such choices, the above calculations show that the claim holds.

8. Discussion and conclusions

Let us further elaborate on the results obtained, together with ideas for possible extensions.

First of all, Theorem 1 provides a global probability estimate for the mixing time bound to hold, but is not an asymptotically almost sure result. It is unclear if this is the result of our bounds being conservative, or because there is truly a large proportion of badly behaving k. Note that there are bad k, for instance if n is even then for $k=n/2$ the mixing time is truly quadratic in n. Indeed, when starting from the distribution $(\delta_{a_1}+\delta_{b_1})/2$ , i.e. weight $\frac 1 2$ on both $a_1,b_1$ , we will observe the evolution of a homogeneous biased random walk on a cycle of length $n/2$ mirrored, the long edge acting simply as a loop. This needs quadratic time to mix in n, improved by a constant as we halved the length. The same reasoning can be applied for $(p/q)n$ for any fixed rational $0<p/q<1$ as $n\to\infty$ . In Figure 6 we observe this non-trivial behavior.

Figure 6. Fluctuation of $t_{\rm mix}\big(\frac 1 4\big)$ depending on the extra edge length k by computer numerical results: (a) for a cycle of $n=2000$ vertices; (b) comparing for various values of n, both normalizing edge lengths and scaling down mixing times with an $n^{3/2}$ factor.

Concerning the proof technique, observe that the grid together with the grid lines correspond to a covering of the original graph which is well suited for our purpose.

An interesting question is whether there is an extension possible for slightly more connections. The more natural one is to increase the number of random edges. In this case, however, we might need to handle the effects of the small permutations generated by the various edges. The more accessible one is to increase the number of random hubs, then add all-to-all connections between them. Closely related work has been done for the asymptotic rate of convergence [10] when then number of hubs can grow at any small polynomial rate, and it turns out that in that case the inverse spectral gap is linear in the length of the arcs (excluding logarithmic factors), which would be a bottleneck anyway.

Still, we might guess the mixing time in a heuristic manner for a constant number of hubs, with the generous assumption that our concepts can be carried over. Let us consider K random hubs – and thus also K arcs – and check mixing until $n^\alpha$ for some $\alpha$ . We can assume the lengths of the arcs are of order n, so the set generalizing R is on a ( $K-1$ )-dimensional hyperplane at a distance of approximately $n^{\alpha-1}$ from the origin. We can hope to get a CLT-type control on the probability in a ball of radius approximately $n^{(\alpha-1)/2}$ again, and thus the number of such points in the hyperplane is approximately $n^{(K-1)(\alpha-1)/2}$ . If once again these map to far away points on the cycle and this movement can be nicely blended together with the diffusion, that would provide an extra factor of approximately $n^{\alpha/2}$ , meaning the total number of vertices reached is approximately $n^{(K-1)({\alpha-1})/{2}+{\alpha}/{2}} = n^{({K}/{2})(\alpha-1)+\frac 1 2}$ . We hope for mixing when the exponent reaches 1, which translates to $\alpha = 1 + 1/K$ , and leads us to the following conjecture.

Conjecture 1. Consider $K\in {\mathbb{Z}}_+$ , ${\varepsilon}>0$ fixed. On a cycle of n vertices, choose K hubs randomly. With an appropriate interconnection structure among the hubs, and a Markov chain otherwise analogous to the one before, there is a positive bounded probability of having $t_{\rm mix}({\varepsilon}) = \Theta\big(n^{1+1/K}\big)$ for n large enough.

In the special case of k random edges, corresponding to $K=2k$ and a perfect matching, the full hyperplane will not be attained, but a similar heuristic computation leads to the following natural conjecture.

Conjecture 2. Consider $k\in {\mathbb{Z}}_+$ , ${\varepsilon}>0$ fixed. On a cycle of n vertices, add k random edges uniformly and independently. As the new edges are disjoint with high probability, we may consider the Markov chain analogous to the one before. Then there is a positive bounded probability of having $t_{\rm mix}({\varepsilon}) = \Theta\big(n^{1+1/(k+1)}\big)$ for n large enough.

Clearly, there is quite some flexibility left for the class of Markov chains to consider. This remains as a question for future research to find out exactly what is needed to generalize the current toolchain.