1 results
WHICH CLASSES OF STRUCTURES ARE BOTH PSEUDO-ELEMENTARY AND DEFINABLE BY AN INFINITARY SENTENCE?
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 15 March 2023, pp. 1-18
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
When classes of structures are not first-order definable, we might still try to find a nice description. There are two common ways for doing this. One is to expand the language, leading to notions of pseudo-elementary classes, and the other is to allow infinite conjuncts and disjuncts. In this paper we examine the intersection. Namely, we address the question: Which classes of structures are both pseudo-elementary and
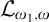${\mathcal {L}}_{\omega _1, \omega }$
-elementary? We find that these are exactly the classes that can be defined by an infinitary formula that has no infinitary disjunctions.
