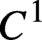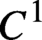Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

physical/srb measures

Ergodic Theory and Dynamical Systems (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

Finitely many physical measures for sectional-hyperbolic attracting sets and statistical stability
Part of
- Dynamical systems with hyperbolic behavior
VITOR ARAUJO
Journal:

Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021

Published online by Cambridge University Press:

30 October 2020, pp. 2706-2733

Print publication:

September 2021
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
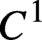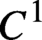We show that a sectional-hyperbolic attracting set for a Hölder- $C^{1}$ vector field admits finitely many physical/SRB measures whose ergodic basins cover Lebesgue almost all points of the basin of topological attraction. In addition, these physical measures depend continuously on the flow in the $C^{1}$ topology, that is, sectional-hyperbolic attracting sets are statistically stable. To prove these results we show that each central-unstable disk in a neighborhood of this class of attracting sets is eventually expanded to contain a ball whose inner radius is uniformly bounded away from zero.