A subset of the Cantor cube is null-additive if its algebraic sum with any null set is null. We construct a set of cardinality continuum such that: all continuous images of the set into the Cantor cube are null-additive, it contains a homeomorphic copy of a set that is not null-additive, and it has the property $\unicode{x3b3} $ , a strong combinatorial covering property. We also construct a nontrivial subset of the Cantor cube with the property $\unicode{x3b3} $ that is not null additive. Set-theoretic assumptions used in our constructions are far milder than used earlier by Galvin–Miller and Bartoszyński–Recław, to obtain sets with analogous properties. We also consider products of Sierpiński sets in the context of combinatorial covering properties.

We define a class of productiveσ-ideals of subsets of the Cantor space 2ω and observe that both σ-ideals of meagre sets and of null sets are in this class. From every productive σ-ideal 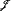we produce a σ-ideal 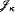of subsets of the generalized Cantor space 2κ. In particular, starting from meagre sets and null sets in 2ω we obtain meagre sets and null sets in 2ω, respectively. Then we investigate additivity, covering number, uniformity and cofinality of 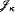. For example, we show that

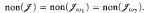
Our results generalizes those from [5].