Cerenkov wake amplification can be used as an accelerating scheme, in which a trigger bunch of electrons propagating inside a cylindrical waveguide filled with an active medium generates an initial wake field. Due to the multiple reflections inside the waveguide, the wake may be amplified significantly more strongly than when propagating in a boundless medium. Sufficiently far away from the trigger bunch the wake, which travels with the same phase velocity as the bunch, reaches saturation and it can accelerate a second bunch of electrons trailing behind.

For a $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{CO}_{2}$ gas mixture our numerical and analytical calculations indicate that a short saturation length and a high gradient can be achieved with a large waveguide radius filled with a high density of excited atoms and a trigger bunch that travels at a velocity slightly above the Cerenkov velocity. To obtain a stable level of saturated wake that will be suitable for particle acceleration, it is crucial to satisfy the single-mode resonance condition, which requires high accuracy in the waveguide radius and the ratio between the electron phase velocity and the Cerenkov velocity. For single-mode propagation our model indicates that it is feasible to obtain gradients as high as 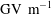$\mathrm{GV\ m}^{-1}$ in a waveguide length of cm.