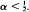The process of software testing usually involves the correction of a detected bug immediately upon detection. In this article, in contrast, we discuss continuous time testing of a software with periodic debugging in which bugs are corrected, instead of at the instants of their detection, at some pre-specified time points. Under the assumption of renewal distribution for the time between successive occurrence of a bug, maximum-likelihood estimation of the initial number of bugs in the software is considered, when the renewal distribution belongs to any general parametric family or is arbitrary. The asymptotic properties of the estimated model parameters are also discussed. Finally, we investigate the finite sample properties of the estimators, specially that of the number of initial number of bugs, through simulation.

In this paper, we propose an estimator of the survival probability for a Lévy risk model observed at low frequency. The estimator is constructed via a regularised version of the inverse of the Laplace transform. The convergence rate of the estimator in a sense of the integrated squared error is studied for large sample size. Simulation studies are also given to show the finite sample performance of our estimator.

Copula function has been widely used in insurance and finance for modeling inter-dependency between risks. Inspired by the Bernstein copula put forward by Sancetta and Satchell (2004, Econometric Theory, 20, 535–562), we introduce a new class of multivariate copulas, the composite Bernstein copula, generated from a composition of two copulas. This new class of copula functions is able to capture tail dependence, and it has a reproduction property for the three important dependency structures: comonotonicity, countermonotonicity and independence. We introduce an estimation procedure based on the empirical composite Bernstein copula which incorporates both prior information and data into the estimation. Simulation studies and an empirical study on financial data illustrate the advantages of the empirical composite Bernstein copula estimation method, especially in capturing tail dependence.

For the construction of bonus-malus systems, we propose to show how to apply, thanks to simple mathematics, a parametric method encompassing those encountered in the literature. We also compare this parametric method with a non-parametric one that has not yet been used in the actuarial literature and that however permits a simple formulation of the stationary and transition probabilities in a portfolio whenever we have the intention to construct a bonus-malus system with finite number of classes.

We consider a random measure for which distribution is invariant under the action of a standard transformation group. The reduced moments are defined by applying classical theorems on invariant measure decomposition. We present a general method for constructing unbiased estimators of reduced moments. Several asymptotic results are established under an extension of the Brillinger mixing condition. Examples related to stochastic geometry are given.

Let ?(u) be the probability of eventual ruin in the classical Sparre Andersen model of risk theory if the initial risk reserve is u. For a large class of such models ?(u) behaves asymptotically like a multiple of exp (–Ru) where R is the adjustment coefficient; R depends on the premium income rate, the claim size distribution and the distribution of the time between claim arrivals. Estimation of R has been considered by many authors. In the present paper we deal with confidence bounds for R. A variety of methods is used, including jackknife estimation of asymptotic variances and the bootstrap. We show that, under certain assumptions, these procedures result in interval estimates that have asymptotically the correct coverage probabilities. We also give the results of a simulation study that compares the different techniques in some particular cases.

Given an i.i.d. sequence X1,X2, … with common distribution function (d.f.) F, the usual non-parametric estimator of F is the e.d.f. Fn; 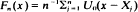where Uo is the d.f. of the unit mass at zero. An admissible perturbation of the e.d.f., say 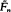, is obtained if Uo is replaced by a d.f. 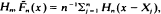, where 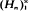is a sequence of d.f.'s converging weakly to Uo. Such perturbed e.d.f.′s arise quite naturally as integrals of non-parametric density estimators, e.g. as 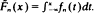. It is shown that if F satisfies some smoothness conditions and the perturbation is not too drastic then 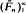‘has the Chung–Smirnov property'; i.e., with probability one, 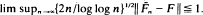1. But if the perturbation is too vigorous then this property is lost: e.g., if F is the uniform distribution and Hn is the d.f. of the unit mass at n–α then the above lim sup is ≦ 1 or = ∞, depending on whethe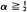r or