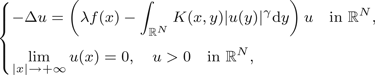1 results
Existence of a Solution for a Non-Local Problem in ℝN via Bifurcation Theory
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 825-845
-
- Article
- Export citation
-
In this paper, we study the existence of a solution for the following class of non-local problems: P
where N ≥ 3, λ > 0, γ ∈ [1, 2), f : ℝ → ℝ is a positive continuous function and K : ℝN × ℝN → ℝ is a non-negative function. The functions f and K satisfy some conditions that permit us to use bifurcation theory to prove the existence of a solution for (P).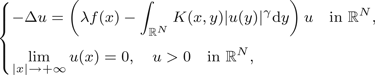
$$\eqalign{\big\{&-\Delta u=\left(\lambda f(x)-\int_{{open R}^N}K(x,y)\vert u(y)\vert ^{\gamma}\hbox{d}y\right)u\quad \mbox{in } \R^{N}, \cr &\lim_{\vert x\vert \to +\infty}u(x)=0,\quad u \gt 0 \quad \text{in } {open R}^{N},}$$
