Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T12:22:12.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of a Solution for a Non-Local Problem in ℝN via Bifurcation Theory

Part of: Elliptic equations and systems Mathematical biology in general

Published online by Cambridge University Press:  21 May 2018

Claudianor O. Alves ,
Romildo N. de Lima  and
Marco A. S. Souto
Claudianor O. Alves
Affiliation:
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58429-900, Campina Grande – PB, Brazil ([email protected]; [email protected]; [email protected])
Romildo N. de Lima*
Affiliation:
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58429-900, Campina Grande – PB, Brazil ([email protected]; [email protected]; [email protected])
Marco A. S. Souto
Affiliation:
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58429-900, Campina Grande – PB, Brazil ([email protected]; [email protected]; [email protected])
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the existence of a solution for the following class of non-local problems: P

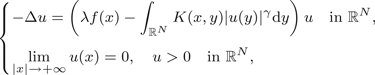$$\eqalign{\big\{&-\Delta u=\left(\lambda f(x)-\int_{{open R}^N}K(x,y)\vert u(y)\vert ^{\gamma}\hbox{d}y\right)u\quad \mbox{in } \R^{N}, \cr &\lim_{\vert x\vert \to +\infty}u(x)=0,\quad u \gt 0 \quad \text{in } {open R}^{N},}$$
where N ≥ 3, λ > 0, γ ∈ [1, 2), f : ℝ → ℝ is a positive continuous function and K : ℝN × ℝN → ℝ is a non-negative function. The functions f and K satisfy some conditions that permit us to use bifurcation theory to prove the existence of a solution for (P).

Keywords

non-local logistic equationsa priori boundspositive solutions

MSC classification

Primary: 35J15: Second-order elliptic equations
Secondary: 35J60: Nonlinear elliptic equations 92B05: General biology and biomathematics
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 3 , August 2018 , pp. 825 - 845
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Allegretto, W. and Nistri, P., On a class of nonlocal problems with applications to mathematical biology, in Differential equations with applications to biology (Halifax, NS, 1997), Fields Institute Communications, Volume 21, pp. 1–14 (American Mathematical Society, Providence, RI, 1999).Google Scholar
2Alves, C. O., Delgado, M., Souto, M. A. S. and Suárez, A., Existence of positive solution of a nonlocal logistic population model, Z. Angew. Math. Phys. 66 (2015), 943–953.CrossRefGoogle Scholar
3Brezis, H., Functional analysis, Sobolev spaces and partial differential equations (Springer, 2010).Google Scholar
4Brezis, H. and Kamin, S., Sublinear elliptic equations in ℝN, Manuscripta Math. 74 (1992), 87–106.Google Scholar
5Chabrowski, J. and Szulkin, A., On the Schrödinger equation involving a critical Sobolev exponent and magnetic field, Top. Meth. Nonlinear Anal. 25 (2005), 3–21.CrossRefGoogle Scholar
6Chen, S. and Shi, J., Stability and Hopf bifurcation in a diffusive logistic population model with nonlocal delay effect, J. Differential Equations 253 (2012), 3440–3470.Google Scholar
7Chipot, M., Remarks on some class of nonlocal elliptic problems, In Recent advances on elliptic and parabolic issues pp. 79–102 (World Scientific, 2006).CrossRefGoogle Scholar
8Corrêa, F. J. S. A., Delgado, M. and Suárez, A., Some nonlinear heterogeneous problems with nonlocal reaction term, Adv. Differential Equations 16 (2011), 623–641.CrossRefGoogle Scholar
9Coville, J., Convergence to equilibrium for positive solutions of some mutation-selection model (arXiv:1308.647; 2013).Google Scholar
10Edelson, A. L. and Rumbos, A. J., Linear and semilinear eigenvalue problems in ℝN, Comm. Partial Differential Equations 18(1–2) (1993), 215–240.Google Scholar
11Edelson, A. L. and Rumbos, A. J., Bifurcation properties of semilinear elliptic equations in ℝN, Differential Integral Equations 6(2) (1994), 399–410.Google Scholar
12Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order (Springer, Berlin, 1998).Google Scholar
13Leman, H., Méléard, S. and Mirrahimi, S., Influence of a spatial structure on the long time behavior of a competitive Lotka-Volterra type system (arXiv: 1401.1182; 2014).Google Scholar
14Rabinowitz, P., Some global results for nonlinear eigenvalue problems, J. Funct. Anal. 7 (1971), 487–513.CrossRefGoogle Scholar
15Sun, L., Shi, J. and Wang, Y., Existence and uniqueness of steady state solutions of a nonlocal diffusive logistic equation, Z. Angew. Math. Phys. 64 (2013), 1267–1278.CrossRefGoogle Scholar