We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that if a countable structure M in a finite relational language is not cellular, then there is an age-preserving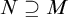 
$N \supseteq M$
such that 
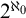$2^{\aleph _0}$
many structures are bi-embeddable with N. The proof proceeds by a case division based on mutual algebraicity.
