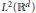A theory of higher rank multiresolution analysis is given in the setting of abelian multiscalings. This theory enables the construction, from a higher rank MRA, of finite wavelet sets whose multidilations have translates forming an orthonormal basis in ${{L}^{2}}({{\mathbb{R}}^{d}})$. While tensor products of uniscaled MRAs provide simple examples we construct many nonseparable higher rank wavelets. In particular we construct Latin square wavelets as rank 2 variants of Haar wavelets. Also we construct nonseparable scaling functions for rank 2 variants of Meyer wavelet scaling functions, and we construct the associated nonseparable wavelets with compactly supported Fourier transforms. On the other hand we show that compactly supported scaling functions for biscaled MRAs are necessarily separable.

Siegmund and Worsley (1995) considered the problem of testing for signals with unknown location and scale in a Gaussian random field defined on ℝN. The test statistic was the maximum of a Gaussian random field in an N+1 dimensional ‘scale space’, N dimensions for location and 1 dimension for the scale of a smoothing filter. Scale space is identical to a continuous wavelet transform with a kernel smoother as the wavelet, though the emphasis here is on signal detection rather than image compression or enhancement. Two methods were used to derive an approximate null distribution for N=2 and N=3: one based on the method of volumes of tubes, the other based on the expected Euler characteristic of the excursion set. The purpose of this paper is two-fold: to show how the latter method can be extended to higher dimensions, and to apply this more general result to χ2 fields. The result of Siegmund and Worsley (1995) then follows as a special case. In this paper the results are applied to the problem of searching for activation in brain images obtained by functional magnetic resonance imaging (fMRI).