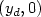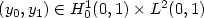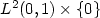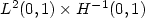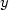2 results
Controllability properties for the one-dimensional Heatequation under multiplicative or nonnegative additive controls with local mobilesupport∗∗∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 27 March 2012, pp. 1207-1224
- Print publication:
- October 2012
-
- Article
- Export citation
Reachability of nonnegative equilibrium statesfor the semilinear vibrating string by varying its axial load and the gain of damping
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 12 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 22 March 2006, pp. 231-252
- Print publication:
- April 2006
-
- Article
- Export citation
-
We show that the set of nonnegative equilibrium-like states, namely, like $ (y_d, 0) $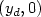
of the semilinear vibrating string that can be reached from any non-zero initial state $ (y_0, y_1) \in H^1_0 (0,1) \times L^2 (0,1)$ 
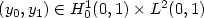, by varying its axial load and the gain of damping, is dense in the “nonnegative” part of the subspace $ L^2 (0,1) \times \{0\} $ 
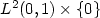of $ L^2 (0,1) \times H^{-1} (0,1)$ 
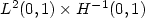. Our main results deal with nonlinear terms which admit at most the linear growth at infinity in $ \; y \; $ 
and satisfy certain restriction on their total impact on (0,∞) with respect to the time-variable.
