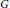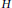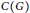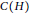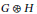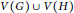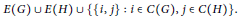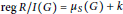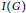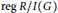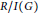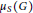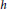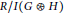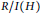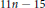The cover product of disjoint graphs 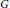$G$ and 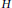$H$ with fixed vertex covers 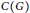$C\left( G \right)$ and 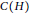$C\left( H \right)$, is the graph 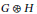$G\circledast H$ with vertex set 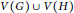$V\left( G \right)\cup V\left( H \right)$ and edge set

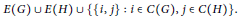$$E\left( G \right)\,\cup \,E\left( H \right)\,\cup \,\left\{ \left\{ i,\,j \right\}\,:\,i\,\in \,C\left( G \right),\,j\,\in \,C\left( H \right) \right\}.$$

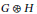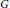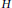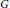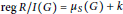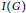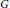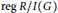We describe the graded Betti numbers of $G\circledast H$ in terms of those of $G$ and $H$. As applications we obtain: (i) For any positive integer k there exists a connected bipartite graph $G$ such that $\text{reg}\,R/I\left( G \right)\,=\,{{\mu }_{s}}\left( G \right)\,+\,k$, where, $I\left( G \right)$ denotes the edge ideal of $G$, $\text{reg}\,\text{R/I}\left( G \right)$ is the Castelnuovo–Mumford regularity of 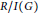$\text{R/I}\left( G \right)$ and 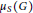${{\mu }_{s}}\left( G \right)$ is the induced or strong matching number of 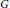$G$; (ii)The graded Betti numbers of the complement of a tree depends only upon its number of vertices; (iii)The 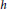$h$-vector of 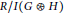$R/I\left( G\circledast H \right)$ is described in terms of the 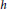$h$-vectors of 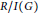$\text{R/I}\left( G \right)$ and 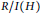$R/I\left( H \right)$. Furthermore, in a different direction, we give a recursive formula for the graded Betti numbers of chordal bipartite graphs.

Multiview geometry is the study of two-dimensional images of three-dimensional scenes, a foundational subject in computer vision. We determine a universal Gröbner basis for the multiview ideal of $n$ generic cameras. As the cameras move, the multiview varieties vary in a family of dimension $11n\,-\,15$. This family is the distinguished component of a multigraded Hilbert scheme with a unique Borel-fixed point. We present a combinatorial study of ideals lying on that Hilbert scheme.

In an earlier work, the authors described a mechanism for lifting monomial ideals to reduced unions of linear varieties. When the monomial ideal is Cohen–Macaulay (including Artinian), the corresponding union of linear varieties is arithmetically Cohen–Macaulay. The first main result of this paper is that if the monomial ideal is Artinian then the corresponding union is in the Gorenstein linkage class of a complete intersection (glicci). This technique has some interesting consequences. For instance, given any (d + 1)-times differentiable O-sequence H, there is a nondegenerate arithmetically Cohen–Macaulay reduced union of linear varieties with Hilbert function H which is glicci. In other words, any Hilbert function that occurs for arithmetically Cohen–Macaulay schemes in fact occurs among the glicci schemes. This is not true for licci schemes. Modifying our technique, the second main result is that any Cohen–Macaulay Borel-fixed monomial ideal is glicci. As a consequence, all arithmetically Cohen–Macaulay subschemes of projective space are glicci up to flat deformation.