1 results
Multiplication Formulas and Canonical Bases for Quantum Affine gln
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 4 / 01 August 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 773-803
- Print publication:
- 01 August 2018
-
- Article
-
- You have access
- Export citation
-
We will give a representation-theoretic proof for the multiplication formula in the Ringel-Hall algebra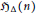
$\mathfrak{H}\vartriangle \,(n)$
of a cyclic quiver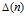 
$\Delta \,(n)$. As a first application, we see immediately the existence of Hall polynomials for cyclic quivers, a fact established by J. Y. Guo and C. M. Ringel, and derive a recursive formula to compute them. We will further use the formula and the construction of a monomial basis for 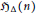$\mathfrak{H}\vartriangle \,(n)$ given by Deng, Du, and Xiao together with the double Ringel-Hall algebra realisation of the quantum loop algebra 
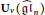${{U}_{v}}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{n}})$ given by Deng, Du, and Fu to develop some algorithms and to compute the canonical basis for 
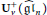$U_{v}^{+}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{n}})$. As examples, we will show explicitly the part of the canonical basis associated with modules of Lowey length at most 2 for the quantum group 
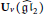${{U}_{v}}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{2}})$.
