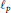1 results
On the Maximal Operator Ideal Associated with a Tensor Norm Defined by Interpolation Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 4 / 01 December 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 690-705
- Print publication:
- 01 December 2010
-
- Article
-
- You have access
- Export citation
-
The classical approach to studying operator ideals using tensor norms mainly focuses on those tensor norms and operator ideals defined by means of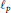
${{l}_{p}}$ spaces. In a previous paper, an interpolation space, defined via the real method and using 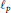${{l}_{p}}$ spaces, was used to define a tensor norm, and the associated minimal operator ideals were characterized. In this paper, the next natural step is taken, that is, the corresponding maximal operator ideals are characterized. As an application, necessary and sufficient conditions for the coincidence of the maximal and minimal ideals are given. Finally, the previous results are used in order to find some new metric properties of the mentioned tensor norm.
